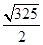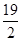题目内容
若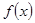
是奇函数，且在区间
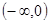上是单调增函数，又
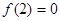，则
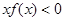的解集为 .
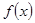是奇函数，且在区间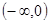上是单调增函数，又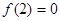，则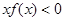的解集为 .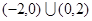
试题分析：根据题意，由于
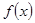是奇函数，则f(-x)=-f(x),且在区间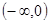上是单调增函数，那么在x>0上递增 ，又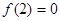,f（-2）=0，那么通过函数图像以及性质可知，当x>0时，f(x)>0,0<x<2;当x>0时，则f(x)<0,则可知-2<x<0，综上可知满足不等式的解集为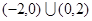点评：主要是考查了函数性质的运用，属于基础题。
练习册系列答案
新课标同步训练系列答案
相关题目
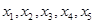均不小于1，且
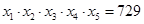，则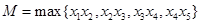
的最小值是 ．（
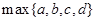是指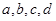
四个数中最大的一个）
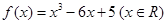，若关于
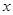的方程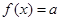
有三个不同实根，则
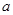的取值范围是 
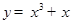的递增区间是（ ）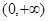
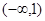
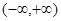
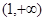
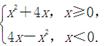若f(2－a2)＞f(a)，则实数a的取值范围是( )
. 
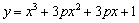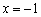处取到极值？若有可能，求实数
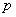的值；否则说明理由；
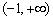上为增函数，求实数
.
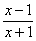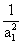)+ln(1+
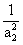)++ln(1+
)>
．
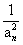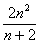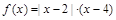在区间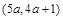
上单调递减，则实数
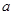的取值范围为______.
