题目内容
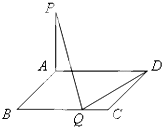如图，已知矩形ABCD中，AB=1，PA⊥平面ABCD，若在BC上有且仅有一个点Q满足PQ⊥DQ，则BC的长是（ ）分析：利用三垂线定理的逆定理、直线与圆相切的判定与性质、矩形的性质、平行线的性质即可求出．
解答：解：连接AQ，取AD的中点O，连接OQ．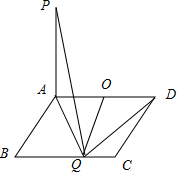
∵PA⊥平面ABCD，PQ⊥DQ，
由三垂线定理的逆定理可得DQ⊥AQ．
∴点Q在以线段AD的中点O为圆心的圆上，
又∵在BC上有且仅有一个点Q满足PQ⊥DQ，∴BC与圆O相切，（否则相交就有两点满足垂直，矛盾．）
∴OQ⊥BC，
∵AD∥BC，∴OQ=AB=1，∴BC=AD=2．
故选D．
∵PA⊥平面ABCD，PQ⊥DQ，
由三垂线定理的逆定理可得DQ⊥AQ．
∴点Q在以线段AD的中点O为圆心的圆上，
又∵在BC上有且仅有一个点Q满足PQ⊥DQ，∴BC与圆O相切，（否则相交就有两点满足垂直，矛盾．）
∴OQ⊥BC，
∵AD∥BC，∴OQ=AB=1，∴BC=AD=2．
故选D．
点评：熟练掌握三垂线定理的逆定理、直线与圆相切的判定与性质、矩形的性质、平行线的性质是解题的关键．
练习册系列答案
相关题目
BC，FO
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。
计20分。请在答题卡指定区域作答。解答应写出文字
说明、证明过程或演算
步骤。
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
在平面直角坐标系xoy中，曲线C的参数方程为
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。
正实数，且ab=2。求证：（1+2a）（1+b）≥9。