题目内容
(2013•青岛二模)已知数列{an}满足a1=1,a1+a2+…+an-1-an=-1(n≥2且n∈N*).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令dn=1+loga
(a>0,a≠1),记数列{dn}的前n项和为Sn,若
恒为一个与n无关的常数λ,试求常数a和λ.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令dn=1+loga
| ||||
| 5 |
| S2n |
| Sn |
分析:(Ⅰ)由a1+a2+…+an-1-an=-1可⇒a1+a2+…+an-an+1=-1,二式作差可得即
=2(n≥2),再求得
=2即可判断数列{an}是首项为1,公比为2的等比数列,从而可求数列{an}的通项公式an;
(Ⅱ)利用等差数列的概念可判断{dn}是以d1=1+2loga2为首项,以2loga2为公差的等差数列,由
=
=λ,结合
恒为一个与n无关的常数λ可得到关于λ的方程组,解之即可.
| an+1 |
| an |
| a2 |
| a1 |
(Ⅱ)利用等差数列的概念可判断{dn}是以d1=1+2loga2为首项,以2loga2为公差的等差数列,由
| S2n |
| Sn |
| 2+(4n+2)loga2 |
| 1+(n+1)loga2 |
| S2n |
| Sn |
解答:解:(Ⅰ)由题a1+a2+…+an-1-an=-1…①
∴a1+a2+…+an-an+1=-1…②
由①-②得:an+1-2an=0,即
=2(n≥2)…(3分)
当n=2时,a1-a2=-1,
∵a1=1,
∴a2=2,
=2,
所以,数列{an}是首项为1,公比为2的等比数列,
故an=2n-1(n∈N*)…(5分)
(Ⅱ)∵an=2n-1,
∴dn=1+loga
=1+2nloga2,
∵dn+1-dn=2loga2,
∴{dn}是以d1=1+2loga2为首项,以2loga2为公差的等差数列,…(8分)
∴
=
=
=λ⇒(λ-4)nloga2+(λ-2)(1+loga2)=0…(10分)
∵
恒为一个与n无关的常数λ,
∴
,
解之得:λ=4,a=
…(12分)
∴a1+a2+…+an-an+1=-1…②
由①-②得:an+1-2an=0,即
| an+1 |
| an |
当n=2时,a1-a2=-1,
∵a1=1,
∴a2=2,
| a2 |
| a1 |
所以,数列{an}是首项为1,公比为2的等比数列,
故an=2n-1(n∈N*)…(5分)
(Ⅱ)∵an=2n-1,
∴dn=1+loga
| ||||
| 5 |
∵dn+1-dn=2loga2,
∴{dn}是以d1=1+2loga2为首项,以2loga2为公差的等差数列,…(8分)
∴
| S2n |
| Sn |
2n(1+2loga2)+
| ||
n(1+2loga2)+
|
=
| 2+(4n+2)loga2 |
| 1+(n+1)loga2 |
∵
| S2n |
| Sn |
∴
|
解之得:λ=4,a=
| 1 |
| 2 |
点评:本题考查等差数列与等比数列的综合,突出考查等差数列与等比数列的通项公式与求和公式的应用,考查转化思想与方程思想,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=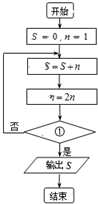 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )