题目内容
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
2
2
.分析:由题意可得当A、P、F共线 时,f(x)取得最小值为
<
,当P与B或C重合时,f(x)取得最大值为
+1>
.g(x)=4f(x)-9的零点的个数就是f(x)=
的解的个数,而由题意可得 f(x)=
的解有2个,从而得出结论.
| 5 |
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
解答:解:由题意可得 函数f(x)=
+
=AP+PF,当A、P、F共线 时,f(x)取得最小值为
<
,当P与B或C重合时,f(x)取得最大值为
+1>
.
g(x)=4f(x)-9=0,即 f(x)=
.故函数g(x)=4f(x)-9的零点的个数就是f(x)=
的解的个数.
而由题意可得 f(x)=
的解有2个,
故答案为 2.
| 1+x2 |
| 1+(1-x)2 |
| 5 |
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
g(x)=4f(x)-9=0,即 f(x)=
| 9 |
| 4 |
| 9 |
| 4 |
而由题意可得 f(x)=
| 9 |
| 4 |
故答案为 2.
点评:本题主要考查方程的根的存在性及个数判断,体现了化归与转化的数学思想,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
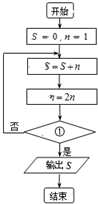 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )