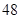题目内容
设p:实数x满足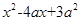 <0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且
<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是
p是 q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.
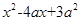 <0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且
<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是
p是 q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.a≤-4或-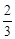 ≤a<0
≤a<0
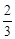 ≤a<0
≤a<0试题分析:解:设A={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},
B={x|x2-x-6≤0或x2+2x-8>0}={x|-2≤x≤3}∪{x|x<-4或x>2}={x|x<-4或x≥-2}.
4分
由
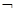 p是
p是 q的必要不充分条件,转化成它的逆否命题q是p的必要不充分条件,即p 是q的充分不必要条件,也就是p
q的必要不充分条件,转化成它的逆否命题q是p的必要不充分条件,即p 是q的充分不必要条件,也就是p q且q
q且q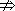 p.
p. 由A
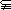 B,得
B,得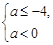 或
或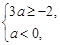 解得a≤-4或-
解得a≤-4或-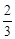 ≤a<0.
≤a<0. 点评:充分条件与必要条件是一个重要的考点。当
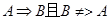 时,A是B的充分不必要条件;当
时,A是B的充分不必要条件;当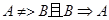 时,A是B的必要不充分条件;当
时,A是B的必要不充分条件;当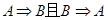 时,A是B的充要条件;当
时,A是B的充要条件;当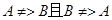 时,A是B的既不充分也不必要条件。
时,A是B的既不充分也不必要条件。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
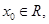 使得
使得
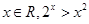
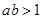 ,则
,则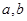 至少有一个大于1
至少有一个大于1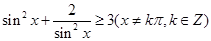
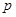 :“
:“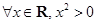 ”,则( )
”,则( )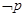 :
: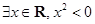
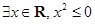

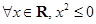
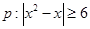 ,
,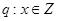 ,若“
,若“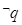 ”为假命题,同时“
”为假命题,同时“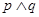 ”也为假命题,求
”也为假命题,求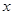 的值
的值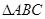 中,“
中,“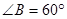 ”是
”是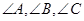 三个角成等差数列的充要条件;
三个角成等差数列的充要条件;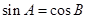 ,则
,则 ”是“
”是“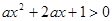 的解集是实数集
的解集是实数集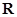 ”的( )
”的( )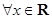 ,
,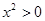 ”的否定是
”的否定是 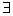
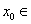 R,
R,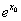
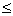 0”的否定是 .
0”的否定是 . 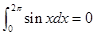 ;
;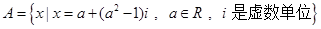 ,若
,若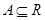 ,则
,则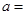 1
1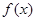 为定义在R上的可导函数,且
为定义在R上的可导函数,且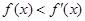 对于
对于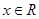 恒成立,则有
恒成立,则有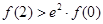 ,
, 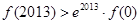 ;
;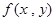 满足:(1)
满足:(1)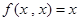 ,(2)
,(2)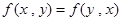 (3)
(3)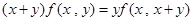 ,则
,则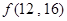 =
=