题目内容
在(x+1)4(x-1)5的展开式中,x3的系数为________.
-4
分析:根据题意,先把(x+1)4(x-1)5变形为(x2-1)4(x-1),分析易得要在(x+1)4(x-1)5出现x3项,必须使(x2-1)4中出现x2项,通过分析(x2-1)4的通项可得x2的系数,结合(x-1)中x的系数,计算可得答案.
解答:(x+1)4(x-1)5=(x2-1)4(x-1),
而(x2-1)4的通项是C4r(-1)r(x2)4-r,
则要(x+1)4(x-1)5出现x3项,必须使(x2-1)4中出现x2项,
只要(x2-1)4的通项中使得r=1,即(-1)3 C41(x2)1,系数是-4,
再乘以后面的x系数为1,得到x3的系数是-4,
故答案为:-4
点评:本题考查二项式定理的运用,解题时注意对(x+1)4(x-1)5变形,由乘法的性质分析,可以避免讨论,简化计算.
分析:根据题意,先把(x+1)4(x-1)5变形为(x2-1)4(x-1),分析易得要在(x+1)4(x-1)5出现x3项,必须使(x2-1)4中出现x2项,通过分析(x2-1)4的通项可得x2的系数,结合(x-1)中x的系数,计算可得答案.
解答:(x+1)4(x-1)5=(x2-1)4(x-1),
而(x2-1)4的通项是C4r(-1)r(x2)4-r,
则要(x+1)4(x-1)5出现x3项,必须使(x2-1)4中出现x2项,
只要(x2-1)4的通项中使得r=1,即(-1)3 C41(x2)1,系数是-4,
再乘以后面的x系数为1,得到x3的系数是-4,
故答案为:-4
点评:本题考查二项式定理的运用,解题时注意对(x+1)4(x-1)5变形,由乘法的性质分析,可以避免讨论,简化计算.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
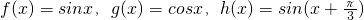 ;
;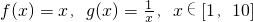 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围. ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.