题目内容
不解三角形,确定下列判断正确的是( )
分析:对于A,由正弦定理可得sinB=
=
,结合b>a,A=45°,可知B有两解;
对于B,根据b<a,A=60°,可得B<A,故B有一解;
对于C,由余弦定理可得c有一解;
对于D,根据a>b,B=120°,可知此时无解.
| bsinA |
| a |
| ||
| 2 |
对于B,根据b<a,A=60°,可得B<A,故B有一解;
对于C,由余弦定理可得c有一解;
对于D,根据a>b,B=120°,可知此时无解.
解答:解:对于A,由正弦定理可得sinB=
=
,∵b>a,A=45°,∴B有两解;
对于B,∵b<a,A=60°,∴B<A,∴B有一解;
对于C,由余弦定理可得c2=3+6-2×
×
×
,∴c有一解;
对于D,∵a>b,B=120°,∴无解
故选C.
| bsinA |
| a |
| ||
| 2 |
对于B,∵b<a,A=60°,∴B<A,∴B有一解;
对于C,由余弦定理可得c2=3+6-2×
| 3 |
| 6 |
| 1 |
| 2 |
对于D,∵a>b,B=120°,∴无解
故选C.
点评:本题考查正弦、余弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
不解三角形,确定下列判断中正确的是( )
| A、a=4,b=5,tanA=2,tanB=3,a=1有一解 | ||||
| B、a=5,b=4,A=60°有两解 | ||||
C、a=
| ||||
D、a=
|
 ,有两解 B.
,有两解 B.  ,有一解
,有一解 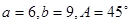 ,有两解 D.
,有两解 D.  ,无解
,无解 ,有一解
,有一解 ,有一解
,有一解 ,有一解
,有一解 ,
, ,B=120°有一解
,B=120°有一解 ,
, ,B=60°一个解
,B=60°一个解