题目内容
不解三角形,确定下列判断中正确的是( )
| A、a=4,b=5,tanA=2,tanB=3,a=1有一解 | ||||
| B、a=5,b=4,A=60°有两解 | ||||
C、a=
| ||||
D、a=
|
分析:根据三角形任意两边之和大于第三边,可得A不正确.根据大边对大角知B<A,题目有唯一解,故B不正确.
由大边对大角,即三角形的内角和可得题目无解,故C不正确.由正弦定理以及大边对大角知三角形有一解,故D正确.
由大边对大角,即三角形的内角和可得题目无解,故C不正确.由正弦定理以及大边对大角知三角形有一解,故D正确.
解答:解:对于A,因为三角形任意两边之和大于第三边,而这里a+c=4+1=5=b,故这样的三角形不存在,故A不正确.
对于B,根据大边对大角知B<A,故B只有一个,故C只有一个,故三角形有一解,故B不正确.
对于C,因为a>b,由于三角形中大边对大角可得A>B=120°,故 A+B>240°,这与三角形的内角和相矛盾,
故本题无解,C不正确.
对于D,由大边对大角知 A<B=60°,故角A只有一个,故角C只有一个,故三角形有唯一解,故D正确.
故选D.
对于B,根据大边对大角知B<A,故B只有一个,故C只有一个,故三角形有一解,故B不正确.
对于C,因为a>b,由于三角形中大边对大角可得A>B=120°,故 A+B>240°,这与三角形的内角和相矛盾,
故本题无解,C不正确.
对于D,由大边对大角知 A<B=60°,故角A只有一个,故角C只有一个,故三角形有唯一解,故D正确.
故选D.
点评:本题考查正弦定理,大边对大角,根据角的正弦值确定角的范围,是解题的难点,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 ,有两解 B.
,有两解 B.  ,有一解
,有一解 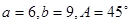 ,有两解 D.
,有两解 D.  ,无解
,无解 ,有一解
,有一解 ,有一解
,有一解 ,有一解
,有一解 ,
, ,B=120°有一解
,B=120°有一解 ,
, ,B=60°一个解
,B=60°一个解