题目内容
(本题满分16分)
已知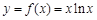 .
.
(1)求函数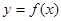 的图像在
的图像在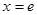 处的切线方程;
处的切线方程;
(2)设实数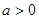 ,求函数
,求函数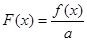 在
在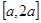 上的最大值.
上的最大值.
(3)证明对一切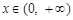 ,都有
,都有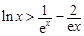 成立.
成立.
已知
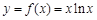 .
.(1)求函数
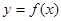 的图像在
的图像在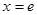 处的切线方程;
处的切线方程;(2)设实数
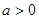 ,求函数
,求函数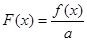 在
在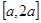 上的最大值.
上的最大值.(3)证明对一切
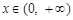 ,都有
,都有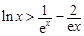 成立.
成立.(1)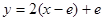 ,即
,即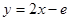
(2)当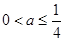 时,
时,
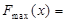
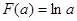
当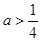 时,
时,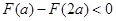 ,
,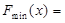
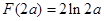
(3)见解析
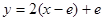 ,即
,即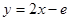
(2)当
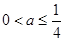 时,
时,
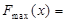
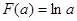
当
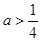 时,
时,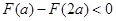 ,
,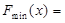
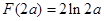
(3)见解析
解:
(1)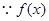 定义域为
定义域为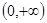
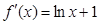
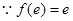 又
又 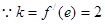
函数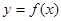 的在
的在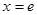 处的切线方程为:
处的切线方程为:
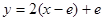 ,即
,即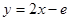 …… 4分
…… 4分
(2)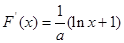 令
令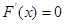 得
得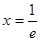
当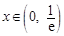 ,
,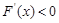 ,
,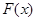 单调递减,
单调递减,
当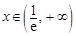 ,
,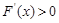 ,
,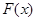 单调递增. ……6分
单调递增. ……6分
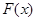 在
在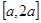 上的最大值
上的最大值

当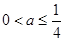 时,
时,
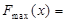
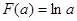
当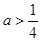 时,
时,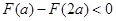 ,
,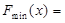
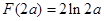 ……10分
……10分
(3)问题等价于证明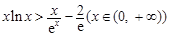 , ……12分
, ……12分
由(2)可知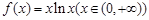 的最小值是
的最小值是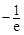 ,当且仅当
,当且仅当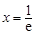 时取得.
时取得.
设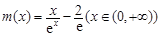 ,则
,则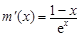 ,易得
,易得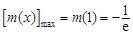 ,
,
当且仅当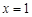 时取到,从而对一切
时取到,从而对一切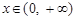 ,都有
,都有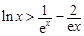 成立. ……16分
成立. ……16分
思路分析:第一问利用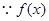 定义域为
定义域为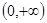
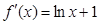
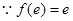
又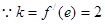 函数
函数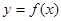 的在
的在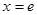 处的切线方程为:
处的切线方程为:
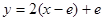 ,即
,即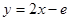
第二问中,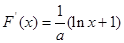 令
令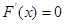 得
得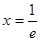
当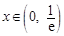 ,
,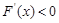 ,
,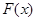 单调递减,
单调递减,
当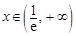 ,
,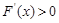 ,
,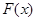 单调递增
单调递增
第三问中,问题等价于证明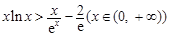 , ……12分
, ……12分
由(2)可知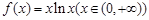 的最小值是
的最小值是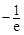 ,当且仅当
,当且仅当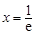 时取得.
时取得.
设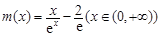 ,则
,则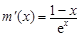 ,易得
,易得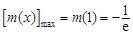
(1)
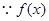 定义域为
定义域为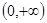
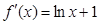
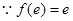 又
又 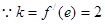
函数
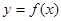 的在
的在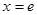 处的切线方程为:
处的切线方程为: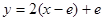 ,即
,即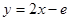 …… 4分
…… 4分(2)
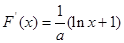 令
令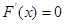 得
得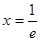
当
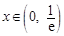 ,
,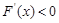 ,
,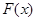 单调递减,
单调递减,当
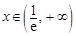 ,
,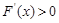 ,
,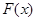 单调递增. ……6分
单调递增. ……6分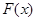 在
在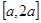 上的最大值
上的最大值

当
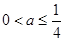 时,
时,
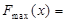
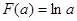
当
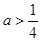 时,
时,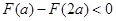 ,
,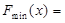
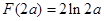 ……10分
……10分(3)问题等价于证明
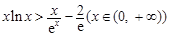 , ……12分
, ……12分由(2)可知
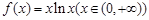 的最小值是
的最小值是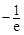 ,当且仅当
,当且仅当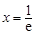 时取得.
时取得. 设
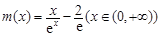 ,则
,则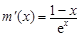 ,易得
,易得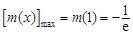 ,
,当且仅当
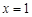 时取到,从而对一切
时取到,从而对一切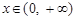 ,都有
,都有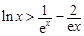 成立. ……16分
成立. ……16分思路分析:第一问利用
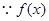 定义域为
定义域为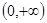
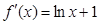
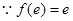
又
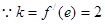 函数
函数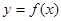 的在
的在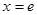 处的切线方程为:
处的切线方程为: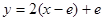 ,即
,即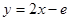
第二问中,
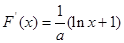 令
令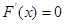 得
得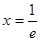
当
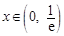 ,
,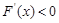 ,
,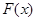 单调递减,
单调递减,当
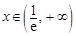 ,
,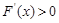 ,
,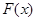 单调递增
单调递增第三问中,问题等价于证明
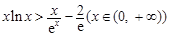 , ……12分
, ……12分由(2)可知
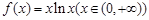 的最小值是
的最小值是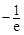 ,当且仅当
,当且仅当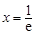 时取得.
时取得. 设
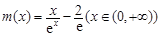 ,则
,则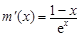 ,易得
,易得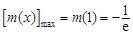

练习册系列答案
相关题目
 则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题:
则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题: ]上具有性质P;
]上具有性质P;
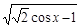 的定义域.
的定义域.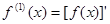 ,
, ,…,
,…,
 .
. ,则
,则 的值为( )
的值为( )



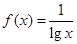 的定义域是 .
的定义域是 .  的定义域是
的定义域是 ,则
,则 的值域是
的值域是  的定义域为
的定义域为 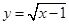 的定义域为
的定义域为

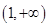
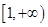
 的定义域是 ;
的定义域是 ;