题目内容
设|a|= 2，|b|=1，a与b夹角为60°，要使kb – a与a垂直，则k的值为（ ）
| A．1 | B．2 | C．3 | D．4 |
D
试题分析：根据题意，由于|a| = 2，|b| =1，a与b夹角为60°，要使kb – a与a垂直，则满足(kb – a）a=0,即可知ab=1,那么可知k-4=0，故可知k=4,答案为D.
点评：本题考点是数量积与向量垂直的关系，直接将垂直关系转化为内积为0，通过解方程的方式求出参数的值，本题型是数量积中的常见题型，是高考的一个热点
练习册系列答案
相关题目
，
，若
，则
=_____________.
与
的夹角为
，则
；
，若
和
的夹角是锐角，则
的取值范围是___ _.
则
、
、
为同平面内具有相同起点的任意三个非零向量，且满足
，
，则
的值一定等于（ ）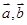
为非零向量，且
，求
与
的夹角
。
的坐标.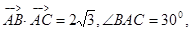
, 则△ABC的面积为（ ）