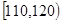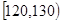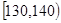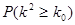题目内容
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
|
分组 |
|
|
|
|
|
|
|
[140,150] |
|
频数 |
2 |
3 |
10 |
15 |
15 |
x |
3 |
1 |
乙校:
|
分组 |
|
|
|
|
|
|
|
[140,150] |
|
频数 |
1 |
2 |
9 |
8 |
10 |
10 |
y |
3 |
(1)计算x,y的值,并分别估计两上学校数学成绩的优秀率;
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
|
|
甲校 |
乙校 |
总计 |
|
优秀 |
|
|
|
|
非优秀 |
|
|
|
|
总计 |
|
|
|
附: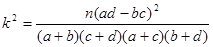
|
|
0.10 |
0.025 |
0.010 |
|
|
2.706 |
5.024 |
6.635 |
解:(1)依题甲校抽取55人,乙校抽取50分, …………2分
故x=6,y=7 …………4分
估计甲校优秀率为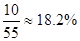
乙校优秀率为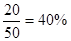 …………6分
…………6分
(2)
|
|
甲校 |
乙校 |
总计 |
|
优秀 |
10 |
20 |
30 |
|
非优秀 |
45 |
30 |
75 |
|
总计 |
55 |
50 |
105 |
…………8分
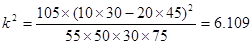 …………10分
…………10分
又因为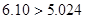 …………11分
…………11分
故有97.5%的把握认为两个学校的数学成绩有差异. …………12分
(注:未经过计算,或计算错误答出有97.5%的把握认为两个学校的数学成绩有差异的同学不得分.)
【解析】略

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案