题目内容
设函数f(θ)=| 3 |
(Ⅰ)若点P的坐标为(
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)若点P(x,y)为平面区域Ω:
|
分析:(I)由已知中函数f(θ)=
sinθ+cosθ,我们将点P的坐标(
,
)代入函数解析式,即可求出结果.
(II)画出满足约束条件
的平面区域,数形结合易判断出θ角的取值范围,结合正弦型函数的性质我们即可求出函数f(θ)的最小值和最大值.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
(II)画出满足约束条件
|
解答:解(I)由点P的坐标和三角函数的定义可得:
于是f(θ)=
sinθ+cosθ=
×
+
=2
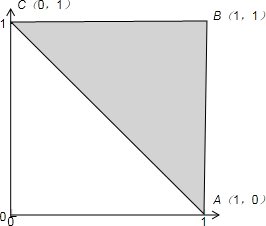 (II)作出平面区域Ω(即感触区域ABC)如图所示
(II)作出平面区域Ω(即感触区域ABC)如图所示
其中A(1,0),B(1,1),C(0,1)
于是0≤θ≤
∴f(θ)=
sinθ+cosθ=2sin(θ+
)
且
≤θ+
≤
故当θ+
=
,即θ=
时,f(θ)取得最大值2
当θ+
=
,即θ=0时,f(θ)取得最小值1
|
于是f(θ)=
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
 (II)作出平面区域Ω(即感触区域ABC)如图所示
(II)作出平面区域Ω(即感触区域ABC)如图所示其中A(1,0),B(1,1),C(0,1)
于是0≤θ≤
| π |
| 2 |
∴f(θ)=
| 3 |
| π |
| 6 |
且
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
故当θ+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
当θ+
| π |
| 6 |
| π |
| 6 |
点评:本题主要考查三角函数、不等式等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.

练习册系列答案
相关题目