Question

设函数f（θ）=

3

sinθ+cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．
（I）若点P的坐标为(

1

2

，

3

2

)，求f（θ）的值；
（II）若点P（x，y）为平面区域Ω：

x+y≥1 x≤1 y≤1

，上的一个动点，试确定角θ的取值范围，并求函数f（θ）的最小值和最大值．

Answer 1

解（I）由点P的坐标和三角函数的定义可得：

sinθ= 3 2 cosθ= 1 2

于是f（θ）=

3

sinθ+cosθ=

3

×

3

2

+

1

2

=2



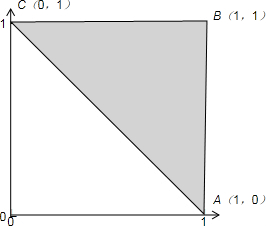
（II）作出平面区域Ω（即感触区域ABC）如图所示
其中A（1，0），B（1，1），C（0，1）
于是0≤θ≤

π

2

∴f（θ）=

3

sinθ+cosθ=2sin(θ+

π

6

)
且

π

6

≤θ+

π

6

≤

2π

3

故当θ+

π

6

=

π

2

，即θ=

π

3

时，f（θ）取得最大值2
当θ+

π

6

=

π

6

，即θ=0时，f（θ）取得最小值1