题目内容
球面上有三个点A、B、C.A和B,A和C间的球面距离等于大圆周长的
.B和C间的球面距离等于大圆周长的
.如果球的半径是R,那么球心到截面ABC的距离等于( )
| 1 |
| 6 |
| 1 |
| 4 |
分析:根据球面上有三点A、B、C,A和B,A和C间的球面距离等于大圆周长的
.B和C间的球面距离等于大圆周长的
,可得OB,OC垂直,AB=AC=R,进而利用截面圆半径,球心距,球半径构成直角三角形,满足勾股定理,得到答案.
| 1 |
| 6 |
| 1 |
| 4 |
解答:解:∵A和B,A和C间的球面距离等于大圆周长的
.B和C间的球面距离等于大圆周长的
.
∴OB⊥OC,AB=AC=OA=OB=OC=R,BC=
R
则△ABC的外接圆半径r=
R
则球心到截面ABC的距离d=
=
R
故选B
| 1 |
| 6 |
| 1 |
| 4 |
∴OB⊥OC,AB=AC=OA=OB=OC=R,BC=
| 2 |
则△ABC的外接圆半径r=
| ||
| 2 |
则球心到截面ABC的距离d=
| R2-r2 |
| ||
| 2 |
故选B
点评:本题考查的知识点是球内接多面体,其中根据截面圆半径,球心距,球半径构成直角三角形,满足勾股定理,构造方程组是解答的关键.

练习册系列答案
相关题目
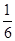 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的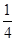 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )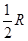 B.
B. 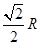 C.
C. 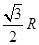 D.
D.