题目内容
一个球面上有三个点A、B、C,若AB=AC=2,BC=2
,球心到平面ABC的距离为1,则球的表面积为( )
| 2 |
分析:根据题意,算出△ABC是以BC为斜边的等腰直角三角形,得BC的中点D为△ABC的外接圆的圆心.设球心为点O,连结OD,由球的截面圆性质,在Rt△BOD中根据所给数据算出OB长,得球半径R=
,即可算出该球的表面积.
| 3 |
解答:解: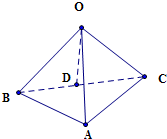 ∵△ABC中,AB=AC=2,BC=2
∵△ABC中,AB=AC=2,BC=2
,
∴AB2+AC2=8=BC2,得△ABC是以BC为斜边的等腰直角三角形.
因此BC的中点D为△ABC的外接圆的圆心,
设球心为点O,连结OD,可得OD⊥平面ABC,
∵球心到平面ABC的距离OD=1,BD=
BC=
,
∴Rt△BOD中,OB=
=
,即球的半径R=
.
由此可得球的表面积S=4πR2=12π.
故选:D
 ∵△ABC中,AB=AC=2,BC=2
∵△ABC中,AB=AC=2,BC=2| 2 |
∴AB2+AC2=8=BC2,得△ABC是以BC为斜边的等腰直角三角形.
因此BC的中点D为△ABC的外接圆的圆心,
设球心为点O,连结OD,可得OD⊥平面ABC,
∵球心到平面ABC的距离OD=1,BD=
| 1 |
| 2 |
| 2 |
∴Rt△BOD中,OB=
| OD2+BD2 |
| 3 |
| 3 |
由此可得球的表面积S=4πR2=12π.
故选:D
点评:本题给出球面上三个点之间的距离,在已知三点确定的平面到球心的距离情况下,求该球的表面积.着重考查了球的截面圆性质、勾股定理和三角形的外接圆等知识,属于中档题.

练习册系列答案
相关题目
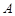 、
、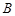 、
、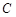 ,若
,若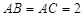 ,
,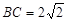 ,球心到平面
,球心到平面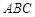 的距离为1,则球的表面积为( )
的距离为1,则球的表面积为( )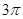 B.
B. C.
C.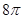 D.
D.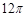
 ,那么这个球的表面积是 .
,那么这个球的表面积是 .