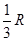题目内容
球面上有三个点A、B、C组成球的一个内接三角形,若AB=18,BC=24,AC=30,且球心到△ABC所在平面的距离等于球半径的
,那么这个球的表面积是
| 1 | 2 |
1200π
1200π
.分析:由已知,易得三角形ABC是直角三角形,AC是斜边,设中点为M,则过A,B,C的截面圆心为M,OA=OB=OC是半径,求出OM,利用球半径是球心O到平面ABC的距离的2倍,求出半径,即可求出球O的表面积.
解答: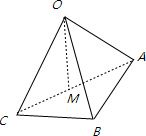 解:球面上三点A、B、C,平面ABC与球面交于一个圆,三点A、B、C在这个圆上
解:球面上三点A、B、C,平面ABC与球面交于一个圆,三点A、B、C在这个圆上
∵AB=18,BC=24,AC=30,
AC2=AB2+BC2,∴AC为这个圆的直径,AC中点M圆心
球心O到平面ABC的距离即OM=球半径的一半=
R
△OMA中,∠OMA=90°,OM=
R,AM=
AC=30×
=15,OA=R
由勾股定理(
R)2+152=R2,
R2=225
解得R=10
球的表面积S=4πR2=1200π
故答案为:1200π.
 解:球面上三点A、B、C,平面ABC与球面交于一个圆,三点A、B、C在这个圆上
解:球面上三点A、B、C,平面ABC与球面交于一个圆,三点A、B、C在这个圆上∵AB=18,BC=24,AC=30,
AC2=AB2+BC2,∴AC为这个圆的直径,AC中点M圆心
球心O到平面ABC的距离即OM=球半径的一半=
| 1 |
| 2 |
△OMA中,∠OMA=90°,OM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理(
| 1 |
| 2 |
| 3 |
| 4 |
解得R=10
| 3 |
球的表面积S=4πR2=1200π
故答案为:1200π.
点评:本题考查空间想象能力,计算能力,根据球的截面圆的性质,确定三角形ABC的形状以及利用球半径是球心O到平面ABC的距离的2倍,是解好本题是前提.

练习册系列答案
相关题目
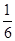 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的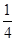 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )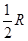 B.
B. 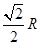 C.
C. 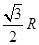 D.
D.