题目内容
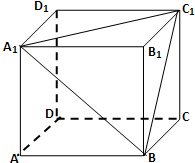 如图,在棱长为1的正方体ABCD-A1B1C1D1中:
如图,在棱长为1的正方体ABCD-A1B1C1D1中:(1)求异面直线BC1与AA1所成的角的大小;
(2)求三棱锥B1-A1C1B的体积.
分析:(1)AA1∥BB1,则异面直线BC1与AA1所成的角就是BC1与BB1所成的角,从而求得∠B1BC1.
(2)根据三棱锥B1-A1C1B的体积=VB-A1B1C1=
S△A1B1C1?BB1进行求解即可.
(2)根据三棱锥B1-A1C1B的体积=VB-A1B1C1=
| 1 |
| 3 |
解答:解:(1):∵AA1∥BB1,
∴异面直线BC1与AA1所成的角就是BC1与BB1所成的角,即∠B1BC1=45°.
故异面直线BC1与AA1所成的角为45°.
(1)V B1-A1C1B=V B-A1B1C1=
S△A1B1C1?BB1=
•
•1•1•1=
.
∴异面直线BC1与AA1所成的角就是BC1与BB1所成的角,即∠B1BC1=45°.
故异面直线BC1与AA1所成的角为45°.
(1)V B1-A1C1B=V B-A1B1C1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题主要考查了直线与平面之间的位置关系,以及几何体的体积和异面直线所成角等有关知识,考查数形结合、化归与转化的数学思想方法,空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
