题目内容
(本小题满分12分)
设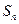 为数列{
为数列{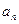 }的前n项和,
}的前n项和,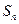 =kn2+n,n∈N*,其中k是常数.
=kn2+n,n∈N*,其中k是常数.
(1)求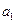 及
及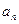 ;
;
(2)若对于任意的m∈N*,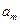 ,
,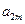 ,
,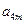 成等比数列,求k的值.
成等比数列,求k的值.
设
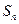 为数列{
为数列{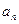 }的前n项和,
}的前n项和,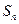 =kn2+n,n∈N*,其中k是常数.
=kn2+n,n∈N*,其中k是常数.(1)求
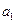 及
及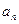 ;
;(2)若对于任意的m∈N*,
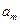 ,
,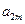 ,
,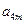 成等比数列,求k的值.
成等比数列,求k的值.(1)
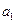 =k+1
=k+1 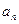 =2kn-k+1,n∈N*
=2kn-k+1,n∈N*(2)k=0,或k=1
(本小题满分12分)
解:(1)由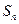 =kn2+n,得
=kn2+n,得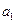 =
=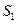 =k+1,
=k+1, 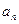 =
=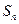 -
-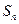 -1=2kn-k+1(n≥2).
-1=2kn-k+1(n≥2).
也满足上式,所以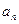 =2kn-k+1,n∈N*.
=2kn-k+1,n∈N*.
(2)由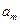 ,
,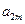 ,
,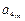 成等比数列,得 (4mk-k+1)2=(2km-k+1)(8km-k+1),
成等比数列,得 (4mk-k+1)2=(2km-k+1)(8km-k+1),
将上式化简,得2km(k-1)=0, 因为m∈N*,所以m≠0,故k=0,或k=1.
解:(1)由
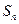 =kn2+n,得
=kn2+n,得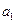 =
=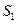 =k+1,
=k+1, 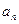 =
=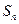 -
-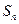 -1=2kn-k+1(n≥2).
-1=2kn-k+1(n≥2).也满足上式,所以
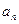 =2kn-k+1,n∈N*.
=2kn-k+1,n∈N*.(2)由
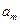 ,
,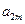 ,
,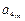 成等比数列,得 (4mk-k+1)2=(2km-k+1)(8km-k+1),
成等比数列,得 (4mk-k+1)2=(2km-k+1)(8km-k+1),将上式化简,得2km(k-1)=0, 因为m∈N*,所以m≠0,故k=0,或k=1.

练习册系列答案
相关题目
 列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。 n=
n= ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。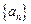 是等比数列,且
是等比数列,且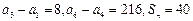 ,求公比
,求公比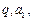 及
及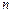 .
.  为等比数列,
为等比数列, ,
, 则
则 ( )
( ) 
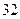

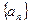 中,前n项和为
中,前n项和为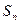 ,若
,若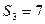 ,
,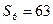 ,则公比
,则公比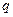 的值是 ( )
的值是 ( ) 中,
中, ,则
,则 =" " ( )
=" " ( )



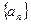 中,
中,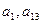 是方程
是方程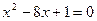 的两个根,则
的两个根,则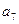 为 ( )
为 ( )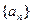 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则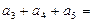 ( )
( )