题目内容
(本小题14分)
已知函数
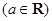 .
.
(Ⅰ)若 ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意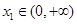 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。
【答案】
解:(Ⅰ)由已知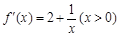 ,……………………………………………………(2分)
,……………………………………………………(2分)
 .
.
故曲线 在
在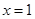 处切线的斜率为
处切线的斜率为 .…………………………………(4分)
.…………………………………(4分)
(Ⅱ)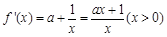 .……………………………………………………(5分)
.……………………………………………………(5分)
①当 时,由于
时,由于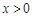 ,故
,故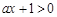 ,
,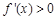
所以,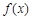 的单调递增区间为
的单调递增区间为 .………………………………………(6分)
.………………………………………(6分)
②当 时,由
时,由 ,得
,得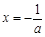 .
.
在区间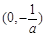 上,
上, ,在区间
,在区间 上
上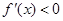 ,
,
所以,函数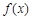 的单调递增区间为
的单调递增区间为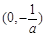 ,单调递减区间为
,单调递减区间为 .………(8分)
.………(8分)
(Ⅲ)由已知,转化为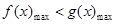 .…………………………………………………(9分)
.…………………………………………………(9分)
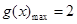 ……………………………………………………………………………(10分)
……………………………………………………………………………(10分)
由(Ⅱ)知,当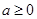 时,
时,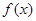 在
在 上单调递增,值域为
上单调递增,值域为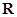 ,故不符合题意.
,故不符合题意.
(或者举出反例:存在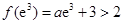 ,故不符合题意.)……………………(11分)
,故不符合题意.)……………………(11分)
当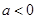 时,
时,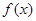 在
在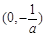 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
故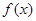 的极大值即为最大值,
的极大值即为最大值, ,…………(13分)
,…………(13分)
所以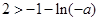 ,
,
解得 . ………………………………………………………………………(14分)
. ………………………………………………………………………(14分)
【解析】略

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中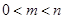 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间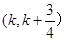 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值