Question

【题目】已知椭圆的左、右焦点分别为、，斜率为1的直线l交椭圆于A、B两点，且线段AB的中点坐标为．

求椭圆的方程；

若P是椭圆与双曲线在第一象限的交点，求的值．

Answer 1

【答案】（1）；（2）.

【解析】

利用点差法得出，结合焦点坐标求出a和b的值，从而可得出椭圆的方程；

先得出椭圆和双曲线共焦点，然后由椭圆和双曲线的定义计算出各边边长，最后利用余弦定理求出的值．

解：设点、，则直线AB的斜率为．

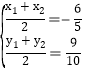由于线段AB的中点坐标为，则有，所以，，

则原点O与线段AB的中点的连线的斜率为．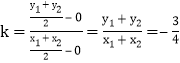

所以，．

将点A、B的坐标代入椭圆的方程得，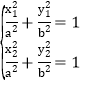

上述两时相减得，，，则，

因此，椭圆的方程为；

双曲线的标准方程为，所以，双曲线的焦点坐标为，则双曲线与椭圆共焦点，

由于点P是双曲线与椭圆在第一象限内的交点，由双曲线和椭圆的定义得，得，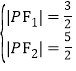

由余弦定理得．