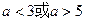题目内容
(本小题满分12分)
已知函数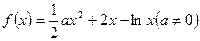
(1)当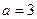 时,求函数
时,求函数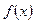 的单调区间;
的单调区间;
(2)若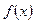 存在单调增区间,求
存在单调增区间,求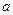 的取值范围。
的取值范围。
已知函数
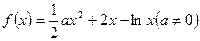
(1)当
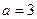 时,求函数
时,求函数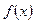 的单调区间;
的单调区间;(2)若
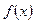 存在单调增区间,求
存在单调增区间,求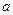 的取值范围。
的取值范围。(1)
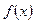 的单调递增区间为
的单调递增区间为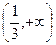 ,
,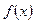 的单调递减区间为
的单调递减区间为
(2)
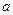 的取值范围
的取值范围
解:(1)

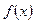 的定义域为
的定义域为 ,
, …………2分
…………2分 …………3分
…………3分所以
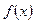 的单调递增区间为
的单调递增区间为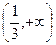 ,
,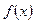 的单调递减区间为
的单调递减区间为 。…………5分
。…………5分(2)
 ,
,若
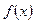 存在单调增区间,则
存在单调增区间,则 在
在 上有解,即
上有解,即 在
在 上有解
上有解设

 ,即
,即 在第一象限内有一段连续的图象…………7分
在第一象限内有一段连续的图象…………7分①当
 时,
时,
 为开口向下的抛物线,对称轴
为开口向下的抛物线,对称轴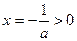 ,
,即为
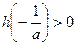 所以
所以 ,即
,即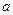 的取值范围
的取值范围 ……………9分
……………9分②当
 时,
时,
 为开口向上的抛物线,
为开口向上的抛物线,因为
 且
且 ,所以
,所以 总有
总有 成立。…………11分
成立。…………11分综上,
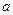 的取值范围
的取值范围 ……………12分
……………12分
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
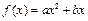 ,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切. 数
数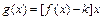 在
在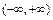 上是单调减函数,那么:求k的取值范围;
上是单调减函数,那么:求k的取值范围;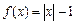 ,关于
,关于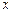 的方程
的方程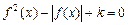 ,若方程恰有8个不同的实根,则实数k的取值范围是 .
,若方程恰有8个不同的实根,则实数k的取值范围是 .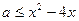 对任意
对任意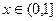 恒成立,则a的取值范围是 ▲ .
恒成立,则a的取值范围是 ▲ .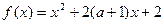 在区间
在区间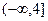 上是减函数,则实数
上是减函数,则实数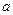 的取值范围是
的取值范围是



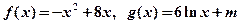 ,要使得
,要使得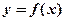 的图象与
的图象与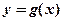 的图象有且只有三个不同的公共点,则实数
的图象有且只有三个不同的公共点,则实数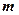 的取值范围是( )
的取值范围是( )



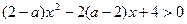 对于一切实数都成立,则( )
对于一切实数都成立,则( )


 或
或
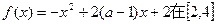 上具有单调性,则实数
上具有单调性,则实数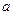 的范围是( )
的范围是( )