题目内容
已知二次函数![]() 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数
均在函数![]() 的图像上。
的图像上。
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() 是数列
是数列![]() 的前n项和,求使得
的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m;
都成立的最小正整数m;
⑴an=6n-5⑵满足要求的最小正整数m为10.
解析:
(1)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点![]() 均在函数
均在函数![]() 的图像上,所以
的图像上,所以![]() =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-![]() =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (![]() )
)
(2)由(1)得知![]() =
=![]() =
=![]() ,
,
故Tn=![]() =
=![]()
![]() =
=![]() (1-
(1-![]() ).
).
因此,要使![]() (1-
(1-![]() )<
)<![]() (
(![]() )成立的m,必须且仅须满足
)成立的m,必须且仅须满足![]() ≤
≤![]() ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.

练习册系列答案
相关题目
 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 均在函数
均在函数 ,
,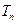 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.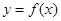 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为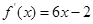 ,数列
,数列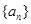 的前n项和为
的前n项和为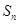 ,点
,点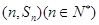 均在函数
均在函数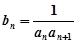 ,
, 是数列
是数列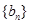 的前n项和,求使得
的前n项和,求使得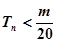 对所有
对所有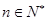 都成立的最小正整数m.
都成立的最小正整数m.