题目内容
已知二次函数![]() 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足![]() ,设函数
,设函数![]() ,其中
,其中![]() 为非零常数
为非零常数
(I)求函数![]() 的解析式;
的解析式;
(II)当![]() 时,判断函数
时,判断函数![]() 的单调性并且说明理由;
的单调性并且说明理由;
(III)证明:对任意的正整数![]() ,不等式
,不等式![]() 恒成立
恒成立
![]()
解析:
(Ⅰ)设![]() ,
,![]() 的图象经过坐标原点,所以c=0.
的图象经过坐标原点,所以c=0.
∵![]() ∴
∴![]()
即:![]()
∴a=1,b=0, ![]() ;……………………………………4分
;……………………………………4分
(Ⅱ)函数![]() 的定义域为
的定义域为
![]() .
.![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,当
,当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上单调递减.………9分
上单调递减.………9分
(III)当![]() 时,
时,![]() ,令
,令![]()
则![]() 在
在![]() 上恒正,
上恒正,
∴![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,恒有
时,恒有![]() .,
.,
即当![]() 时,有
时,有![]()
![]() ,
,
对任意正整数![]() ,取
,取![]() 得
得![]() .………………13分
.………………13分

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 均在函数
均在函数 ,
,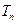 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.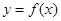 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为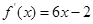 ,数列
,数列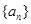 的前n项和为
的前n项和为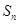 ,点
,点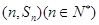 均在函数
均在函数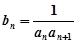 ,
, 是数列
是数列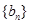 的前n项和,求使得
的前n项和,求使得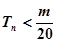 对所有
对所有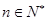 都成立的最小正整数m.
都成立的最小正整数m.