题目内容
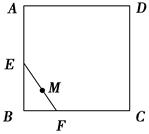
现有一张长为80 cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x(cm),高为y(cm),体积为V(cm3)

(1)求出x与 y的关系式;
(2)求该铁皮盒体积V的最大值.

(1)求出x与 y的关系式;
(2)求该铁皮盒体积V的最大值.
(1)y=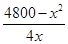 ,0<x<60.(2)32000 cm3
,0<x<60.(2)32000 cm3
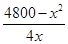 ,0<x<60.(2)32000 cm3
,0<x<60.(2)32000 cm3(1)由题意得x2+4xy=4 800,
即y=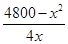 ,0<x<60.
,0<x<60.
(2)铁皮盒体积V(x)=x2y=x2×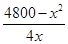 =-
=-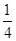 x3+1 200x,V′(x)=-
x3+1 200x,V′(x)=-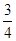 x2+1200,令V′(x)=0,得x=40,因为x∈(0,40),V′(x)>0,V(x)是增函数;x∈(40,60),V′(x)<0,V(x)是减函数,所以V(x)=-
x2+1200,令V′(x)=0,得x=40,因为x∈(0,40),V′(x)>0,V(x)是增函数;x∈(40,60),V′(x)<0,V(x)是减函数,所以V(x)=-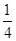 x3+1 200x,在x=40时取得极大值,也是最大值,其值为32 000 cm3.
x3+1 200x,在x=40时取得极大值,也是最大值,其值为32 000 cm3.
所以该铁皮盒体积V的最大值是32000 cm3.
即y=
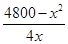 ,0<x<60.
,0<x<60.(2)铁皮盒体积V(x)=x2y=x2×
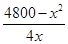 =-
=-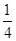 x3+1 200x,V′(x)=-
x3+1 200x,V′(x)=-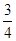 x2+1200,令V′(x)=0,得x=40,因为x∈(0,40),V′(x)>0,V(x)是增函数;x∈(40,60),V′(x)<0,V(x)是减函数,所以V(x)=-
x2+1200,令V′(x)=0,得x=40,因为x∈(0,40),V′(x)>0,V(x)是增函数;x∈(40,60),V′(x)<0,V(x)是减函数,所以V(x)=-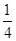 x3+1 200x,在x=40时取得极大值,也是最大值,其值为32 000 cm3.
x3+1 200x,在x=40时取得极大值,也是最大值,其值为32 000 cm3.所以该铁皮盒体积V的最大值是32000 cm3.

练习册系列答案
相关题目
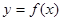 的周期为2,当
的周期为2,当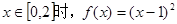 ,如果
,如果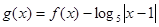 ,则函数
,则函数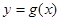 的所有零点之和为( )
的所有零点之和为( )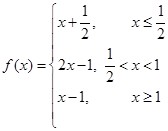 ,若数列
,若数列 满足
满足 ,则
,则




 ,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.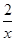 的零点,则[x0]=________.
的零点,则[x0]=________.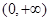 上单调递增的是( )
上单调递增的是( )


