题目内容
(选做题)
(Ⅰ) 设a1,a2,a3均为正数,且a1+a2+a3=m,求证 +
+ +
+ ≥
≥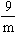 .
.
(Ⅱ) 已知a,b都是正数,x,y∈R,且a+b=1,求证:ax2+by2≥(ax+by)2.
(Ⅰ) 设a1,a2,a3均为正数,且a1+a2+a3=m,求证
 +
+ +
+ ≥
≥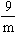 .
.(Ⅱ) 已知a,b都是正数,x,y∈R,且a+b=1,求证:ax2+by2≥(ax+by)2.
证明:(I)∵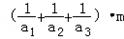 =
=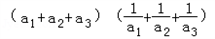
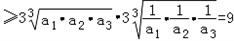 ,
,
当且仅当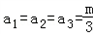 时等号成立.
时等号成立.
又∵m=a1+a2+a3>0,
∴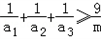 .
.
(II)ax2+by2=(ax2+by2)(a+b)=a2x2+b2y2+ab(x2+y2)≥a2x2+b2y2+2abxy=(ax+by)2.
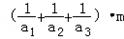 =
=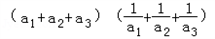
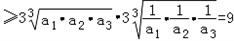 ,
,当且仅当
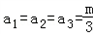 时等号成立.
时等号成立.又∵m=a1+a2+a3>0,
∴
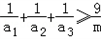 .
.(II)ax2+by2=(ax2+by2)(a+b)=a2x2+b2y2+ab(x2+y2)≥a2x2+b2y2+2abxy=(ax+by)2.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
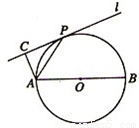
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分. (选做题)如图,设直线l切⊙O于点P,AB为⊙O的任一条不与l垂直的直径,AC⊥l,垂足为点C.
(选做题)如图,设直线l切⊙O于点P,AB为⊙O的任一条不与l垂直的直径,AC⊥l,垂足为点C.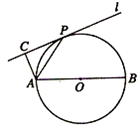 (选做题)如图,设直线l切⊙O于点P,AB为⊙O的任一条不与l垂直的直径,AC⊥l,垂足为点C.
(选做题)如图,设直线l切⊙O于点P,AB为⊙O的任一条不与l垂直的直径,AC⊥l,垂足为点C.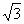 (θ为参数)表示的曲线为C,则曲线C上的动点到原点O的距离的最小值为______________.
(θ为参数)表示的曲线为C,则曲线C上的动点到原点O的距离的最小值为______________.