Question

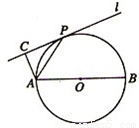
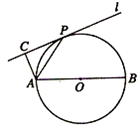（选做题）如图，设直线l切⊙O于点P，AB为⊙O的任一条不与l垂直的直径，AC⊥l，垂足为点C．
求证：AP平分∠CAB．

Answer 1

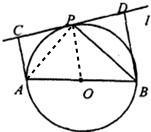证明：连接BP，
因为l是⊙O的切线，
所以∠BPD=∠BAP．
又∠BPD+∠APC=90°，
∠APC+∠PAC=90°，
所以∠BPD=∠PAC，
∴∠PAC=∠BAP
即PA平分∠CAB．
分析：要想得到AP平分∠CAB，即证∠PAC=∠BAP，观察到已知中及图中有多个垂直关系，又由AB为直径也可得到∠APB=90°，故可以结合弦切角定理，利用等量代换的思想解决问题．
点评：本小题主要考查弦切角、圆周角定理等基础知识，考查根据已知条件分析转化的思想，属于基础题．