题目内容
在平面直角坐标系中，若定点A（1，2）与动点P（x，y）满足向量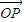
在向量
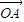上的投影为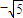
，则点P的轨迹方程是（ ）A．x-2y+5=0
B．x+2y-5=0
C．x+2y+5=0
D．x-2y-5=0
【答案】分析：根据向量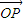
在向量
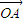上的投影为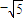
，可得关系x，y的一方程，化简即为所求轨迹方程．
解答：解：由于定点A（1，2）与动点P（x，y）满足向量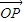
在向量
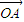上的投影为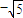
，
根据向量投影定义得，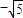
=
=
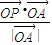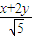，即x+2y+5=0，
∴点P的轨迹方程是x+2y+5=0，
故选C．
点评：本题考查轨迹方程的求法及向量投影的定义，本题中轨迹方程的求解采取直接法，理解向量投影定义是解决本题的关键．
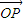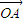在向量上的投影为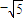，可得关系x，y的一方程，化简即为所求轨迹方程．解答：解：由于定点A（1，2）与动点P（x，y）满足向量
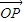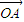在向量上的投影为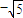，根据向量投影定义得，
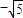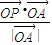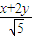==，即x+2y+5=0，∴点P的轨迹方程是x+2y+5=0，
故选C．
点评：本题考查轨迹方程的求法及向量投影的定义，本题中轨迹方程的求解采取直接法，理解向量投影定义是解决本题的关键．
练习册系列答案
相关题目