题目内容
(1)已知a=8,b=-2,求[a-| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
(2)已知x
| 1 |
| 2 |
| 1 |
| 2 |
x
| ||||
| x2+x-2+3 |
分析:(1)利用幂的运算法则化简式子,再将a,b的值代入求出值.
(2)①将已知等式平方求出x+x-1
②利用立方和公式及完全平方公式将待求的式子用x+x-1及x
+x-
表示,求出值.
(2)①将已知等式平方求出x+x-1
②利用立方和公式及完全平方公式将待求的式子用x+x-1及x
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)[a-
b(ab-2)-
(a-1)-
]2=[a-
-
+
•b1+1]2=a-
b4=4;
(2)①∵x
+x-
=3
平方得x+x-1+2=9
∴x+x-1=7
②
=
=
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
(2)①∵x
| 1 |
| 2 |
| 1 |
| 2 |
平方得x+x-1+2=9
∴x+x-1=7
②
x
| ||||
| x2+x-2+3 |
=
(x
| ||||
| (x+x-1)2+1 |
=
| 3×6+2 |
| 49+1 |
=
| 2 |
| 5 |
点评:本题考查同底数幂的运算法则、完全平方公式、立方和公式.

练习册系列答案
相关题目
 的值.
的值.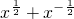 =3,求下列各式的值:①x+x-1;②
=3,求下列各式的值:①x+x-1;②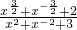 .
.