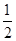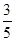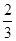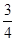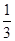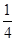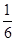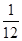题目内容
有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同且互不相干,则这两位同学恰参加同一兴趣小组的概率为 ( )
A.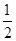 | B.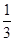 | C. | D. |
B
解析试题分析:由题意知本题是一个古典概型,试验发生包含的事件数是3×3=9种结果,
满足条件的事件是这两位同学参加同一个兴趣小组有3种结果,
根据古典概型概率公式得到P= ,故选B.
,故选B.
考点:本题主要考查古典概型概率的计算。
点评:简单题,使用列举法、“树图法”、“坐标法”等,确定得到试验发生包含的事件数和满足条件的事件数。

练习册系列答案
相关题目
已知正三棱锥 的底面边长为
的底面边长为 ,高为
,高为 ,在正三棱锥内任取一点
,在正三棱锥内任取一点 ,使得
,使得 的概率为( )
的概率为( )
A. | B. | C. | D. |
若 是离散型随机变量,
是离散型随机变量,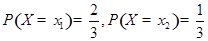 ,且
,且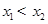 ,又已知
,又已知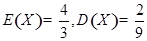 ,则
,则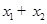 的值为( )
的值为( )
A.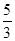 | B.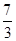 | C. | D.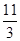 |
设随机变量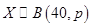 ,且
,且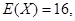 则
则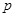 等于( )
等于( )
A.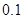 | B.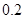 | C.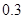 | D.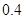 |
下列叙述正确的是
A.任何事件的概率总是在 之间 之间 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增加,频率一般会越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
| A.至少有一个红球与都是红球 |
| B.至少有一个红球与都是白球 |
| C.至少有一个红球与至少有一个白球 |
| D.恰有一个红球与恰有二个红球 |
在区间[0,6]上随机取一个数x,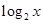 的值介于0到2之间的概率为( )
的值介于0到2之间的概率为( )
A.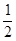 | B.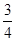 | C.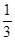 | D. |