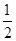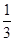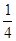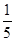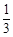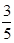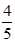题目内容
若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在直线x+y=4上的概率是( )
A.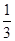 | B.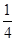 | C.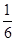 | D.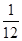 |
D
解析试题分析:利用分布计数原理求出所有的基本事件个数,在求出点落在直线x+y=4上包含的基本事件个数,利用古典概型的概率个数求出. 解:连续抛掷两次骰子出现的结果共有6×6=36,其中每个结果出现的机会都是等可能的,点P(m,n)在直线x+y=4上包含的结果有(1,3),(2,2),(3,1)共三个,所以点P(m,n)在直线x+y=4上的概率是3:36=1:12,故选D.
考点:古典概型
点评:本题考查先判断出各个结果是等可能事件,再利用古典概型的概率公式求概率,属于基础题。

练习册系列答案
相关题目
已知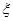 ~
~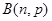 ,且
,且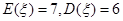 ,则
,则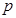 等于( )
等于( )
A.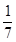 | B.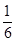 | C.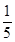 | D.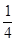 |
一件产品要经过2道独立的加工工序,第一道工序的次品率为a,第二道工序的次品率为b,则产品的正品率为( ):
| A. 1-a-b | B.1-a·b |
| C.(1-a)·(1-b) | D.1-(1-a)·(1-b) |
已知随机变量X服从正态分布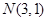 ,且
,且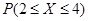 =0.6826,则
=0.6826,则 =( )
=( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
把一枚硬币连续抛掷两次,事件 “第一次出现正面”,事件
“第一次出现正面”,事件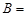 “第二次出现正面”,则
“第二次出现正面”,则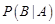 等于( )
等于( )
A.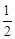 | B.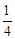 | C. | D. |
在区间 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为( ).
之间的概率为( ).
A. | B. | C. | D. |