题目内容
双曲线C1：
＝1(m>0，b>0)与椭圆C2：
＝1(a>b>0)有相同的焦点，双曲线C1的离心率是e1，椭圆C2的离心率是e2，则
＋
( )．
A. 
B．1 C. 
D．2
D
【解析】在双曲线的方程中c2＝m2＋b2，在椭圆的方程中c2＝a2－b2，所以c2＝a2－b2＝m2＋b2，即m2＝a2－2b2，所以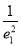
＋
＝
＝
＝
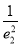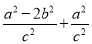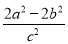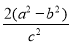＝2.
练习册系列答案
相关题目
题目内容
双曲线C1：＝1(m>0，b>0)与椭圆C2：＝1(a>b>0)有相同的焦点，双曲线C1的离心率是e1，椭圆C2的离心率是e2，则＋( )．
A. B．1 C. D．2
D
【解析】在双曲线的方程中c2＝m2＋b2，在椭圆的方程中c2＝a2－b2，所以c2＝a2－b2＝m2＋b2，即m2＝a2－2b2，所以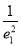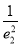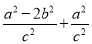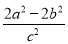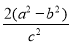＋＝＝＝＝2.
