题目内容
已知函数 ,
,
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设 的内角
的内角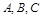 的对边分别
的对边分别 且
且 ,
, ,若
,若 求
求 的值.
的值.
 ,
,
(Ⅰ)求函数
 的最大值和最小正周期;
的最大值和最小正周期;(Ⅱ)设
 的内角
的内角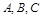 的对边分别
的对边分别 且
且 ,
, ,若
,若 求
求 的值.
的值.(Ⅰ)0,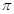 (Ⅱ)
(Ⅱ)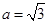
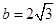
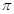 (Ⅱ)
(Ⅱ)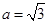
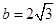
本题考查三角函数的化简,考查三角函数的性质,考查正弦、余弦定理的运用,属于中档题.
(1)利用二倍角公式、辅助角公式化简三角函数,即可求函数f(x)的最大值和最小正周期;
(2)先求出C,再利用sin(A+C)=2sinA,结合正弦、余弦定理,可求a,b的值.
解:(1)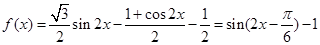 …………….3分
…………….3分
则 的最大值为0,最小正周期是
的最大值为0,最小正周期是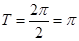 …………………6分
…………………6分
(2)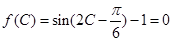 则
则


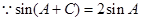 由正弦定理得
由正弦定理得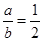 ①………………………9分
①………………………9分
由余弦定理得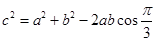
即 ②
②
由①②解得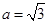
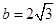 ………………12分
………………12分
(1)利用二倍角公式、辅助角公式化简三角函数,即可求函数f(x)的最大值和最小正周期;
(2)先求出C,再利用sin(A+C)=2sinA,结合正弦、余弦定理,可求a,b的值.
解:(1)
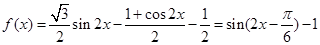 …………….3分
…………….3分则
 的最大值为0,最小正周期是
的最大值为0,最小正周期是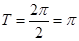 …………………6分
…………………6分(2)
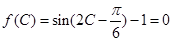 则
则


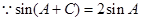 由正弦定理得
由正弦定理得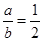 ①………………………9分
①………………………9分由余弦定理得
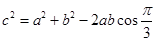
即
 ②
②由①②解得
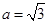
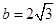 ………………12分
………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
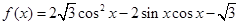 ,
,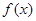 的单调递增区间.
的单调递增区间.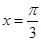 处的切线方程.
处的切线方程. 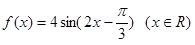 ,有下列命题:
,有下列命题: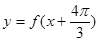 为偶函数,
为偶函数,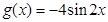 的图像,只需将
的图像,只需将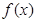 的图像向右平移
的图像向右平移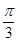 个单位,
个单位,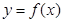 的图像关于直线
的图像关于直线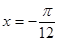 对称.
对称.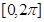 内的增区间为
内的增区间为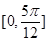 和
和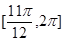 ;
; 的图象,只需要把函数
的图象,只需要把函数 的图象上所有的点 ( )
的图象上所有的点 ( )

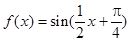 ,求函数在区间
,求函数在区间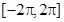 上的单调增区间;
上的单调增区间;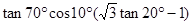 .
. 的对边长分别为a、b、c,已知a、b、c成等比数列,且
的对边长分别为a、b、c,已知a、b、c成等比数列,且
 的大小;
的大小; ,求函数
,求函数 的值域.
的值域.  的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 单位长度,所得图象的函数解析式是( )
单位长度,所得图象的函数解析式是( )



 )+sin(
)+sin( )的图象的相邻两对称轴之间的距离是______.
)的图象的相邻两对称轴之间的距离是______.
 的最小正周期和最小值;
的最小正周期和最小值; 的内角
的内角 对边分别为
对边分别为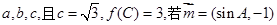 与
与 垂直,求
垂直,求 的值.
的值.