题目内容
17.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的右顶点为A,上、下顶点分别为 B2、B1,左、右焦点分别是F1、F2,若直线 B1F2与直线 AB2交于点 P,且∠B1PA为锐角,则离心率的范围是$0<e<\frac{{-1+\sqrt{5}}}{2}$.分析 由题意,∠B1PA就是$\overrightarrow{{B}_{2}A}$与$\overrightarrow{{F}_{2}{B}_{1}}$的夹角,设椭圆的长半轴、短半轴、半焦距分别为a,b,c,则$\overrightarrow{{B}_{2}A}$=(a,-b)、$\overrightarrow{{F}_{2}{B}_{1}}$=(-c,-b),由向量的夹角为锐角可得-ac+b2>0,把b2=a2-c2代入不等式,从而可求椭圆离心率的取值范围.
解答 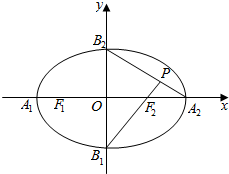 解:由题意,∠B1PA就是$\overrightarrow{{B}_{2}A}$与$\overrightarrow{{F}_{2}{B}_{1}}$的夹角,
解:由题意,∠B1PA就是$\overrightarrow{{B}_{2}A}$与$\overrightarrow{{F}_{2}{B}_{1}}$的夹角,
设椭圆的长半轴、短半轴、半焦距分别为a,b,c,
则$\overrightarrow{{B}_{2}A}$=(a,-b)、$\overrightarrow{{F}_{2}{B}_{1}}$=(-c,-b),
由向量的夹角为锐角,知道$\overrightarrow{{B}_{2}A}$与$\overrightarrow{{F}_{2}{B}_{1}}$的数量积大于0,
所以有:-ac+b2>0,
把b2=a2-c2代入不等式得:a2-ac-c2>0,
除以a2得1-e-e2>0,
即e2+e-1<0,解得$\frac{-1-\sqrt{5}}{2}$<e<$\frac{\sqrt{5}-1}{2}$,
又0<e<1,所以0<e<$\frac{\sqrt{5}-1}{2}$,
故答案为:0<e<$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的几何性质,解题的关键是利用$\overrightarrow{{B}_{2}A}$与$\overrightarrow{{F}_{2}{B}_{1}}$的数量积大于0,建立不等式,属于中档题.

| A. | $\frac{x^2}{25}+\frac{{9{y^2}}}{100}=1(x≠±5)$ | B. | $\frac{x^2}{25}+\frac{{100{y^2}}}{9}=1(x≠±5)$ | ||
| C. | $\frac{x^2}{25}-\frac{{9{y^2}}}{100}=1(y≠0)$ | D. | $\frac{x^2}{25}-\frac{{100{y^2}}}{9}=1(y≠0)$ |
| A. | {4,5,6,7} | B. | {4,5,6} | C. | {3,4,5,6} | D. | {3,4,5,6,7} |

| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
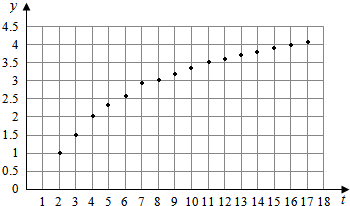 一项实验中获得的一组关于变量y,t之间的数据整理后得到如图所示的散点图.下列函数中可以
一项实验中获得的一组关于变量y,t之间的数据整理后得到如图所示的散点图.下列函数中可以近视刻画y与t之间关系的最佳选择是( )
| A. | y=at | B. | y=logat | C. | y=at3 | D. | y=a$\sqrt{t}$ |