题目内容
设函数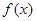 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数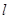 使得对于任意
使得对于任意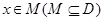 ,有
,有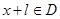 ,且
,且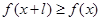 ,则称
,则称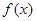 为M上的
为M上的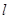 高调函数.
高调函数.
现给出下列命题:
① 函数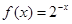 为R上的1高调函数;
为R上的1高调函数;
② 函数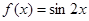 为R上的
为R上的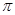 高调函数;
高调函数;
③ 如果定义域为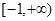 的函数
的函数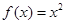 为
为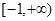 上
上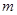 高调函数,那么实数
高调函数,那么实数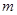 的取值范围是
的取值范围是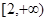 ;
;
④ 函数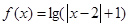 为
为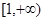 上的2高调函数。
上的2高调函数。
其中真命题的个数为
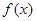 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数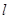 使得对于任意
使得对于任意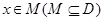 ,有
,有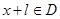 ,且
,且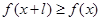 ,则称
,则称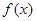 为M上的
为M上的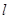 高调函数.
高调函数. 现给出下列命题:
① 函数
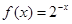 为R上的1高调函数;
为R上的1高调函数;② 函数
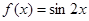 为R上的
为R上的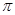 高调函数;
高调函数;③ 如果定义域为
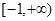 的函数
的函数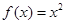 为
为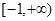 上
上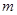 高调函数,那么实数
高调函数,那么实数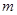 的取值范围是
的取值范围是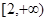 ;
;④ 函数
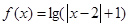 为
为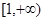 上的2高调函数。
上的2高调函数。其中真命题的个数为
| A.0 | B.1 | C.2 | D.3 |
D
试题分析:首先理解“高调函数”的定义:函数
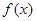 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数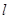 使得对于任意
使得对于任意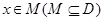 ,有
,有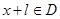 ,且
,且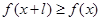 ,则称
,则称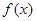 为M上的
为M上的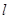 高调函数.
高调函数.据此研究四个函数:
对于①,即f(x)=(
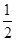 )x。f(x+l)=(
)x。f(x+l)=(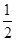 )x+l,要使f(x+l)≥f(x),需要(
)x+l,要使f(x+l)≥f(x),需要(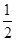 )x+l≥(
)x+l≥(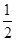 )x恒成立,只需l≤0;所以①函数
)x恒成立,只需l≤0;所以①函数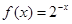 为R上的1高调函数;不对;
为R上的1高调函数;不对;对于②,f(x+1))=sin2(x+1)≥sin2x=f(x),当l=π时恒成立;所以函数f(x)=sin2x为R上的π高调函数,
所以②对;
对于③,f(x+m)=(x+m)2,f(x)=x2,令(x+m)2≥x2,即2mx+m2≥0在
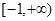 恒成立,
恒成立,∴m>0且2m(-1)+m2≥0,解得m≥2,故③对;
对于④ 函数
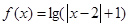 ,若其为2高调函数,
,若其为2高调函数,则由
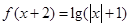 ≥
≥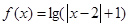 ,在
,在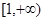 恒成立,
恒成立,得
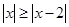 在
在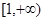 恒成立,而此恒成立,所以④对
恒成立,而此恒成立,所以④对故正确的命题个数是3个,
故选D。
点评:新定义问题,具有较强的综合性。关键是阅读理解新定义内容,应用知识分析解决问题,利用数形结合的方法,应用图象解决问题,属中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
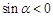 ,则角
,则角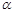 的终边在第三、四象限;②若点
的终边在第三、四象限;②若点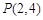 在函数
在函数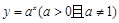 的图象上,则点
的图象上,则点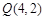 必在函数
必在函数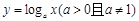 的图象上;③若角
的图象上;③若角 的终边成一条直线,则
的终边成一条直线,则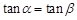 ;④幂函数的图象必过点(1,1)与(0,0).其中所有正确命题的序号是
;④幂函数的图象必过点(1,1)与(0,0).其中所有正确命题的序号是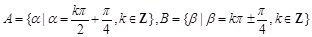 ,则
,则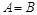 ;
;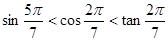
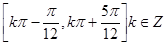 是函数
是函数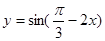 的单调递减区间
的单调递减区间 的周期和对称轴方程分别为
的周期和对称轴方程分别为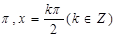
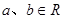 ,都有
,都有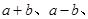
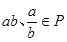 (除数
(除数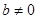 ),则称P是一个数域.例如有理数集Q是数域;数集
),则称P是一个数域.例如有理数集Q是数域;数集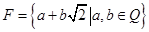 也是数域.有下列命题:
也是数域.有下列命题: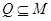 ,则数集M必为数域;
,则数集M必为数域;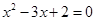 ,则
,则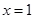 ”的逆否命题为“若
”的逆否命题为“若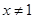 ,则
,则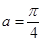 ”是“
”是“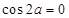 ”的充分不必要条件;
”的充分不必要条件;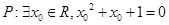 ,则
,则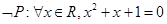 ;
;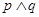 为假,
为假,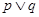 为真,则
为真,则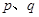 有且仅有一个是真命题.
有且仅有一个是真命题. ,使得
,使得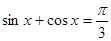 ;
;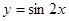 的图象向右平移
的图象向右平移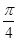 个单位,得到
个单位,得到 的图象;
的图象;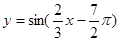 是偶函数;
是偶函数;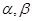 是锐角三角形ABC的两个内角,则
是锐角三角形ABC的两个内角,则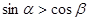 。
。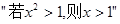 的否命题为
的否命题为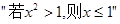 。
。 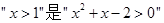 的充分不必要条件 。
的充分不必要条件 。 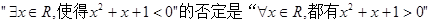 。
。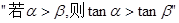 的逆命题为真命题。
的逆命题为真命题。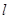 为一条直线,
为一条直线,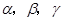 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题: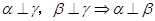 ;②
;②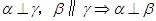 ;③
;③ .其中正确的命题有( )
.其中正确的命题有( )