题目内容
成都市某物流公司为了配合“北改”项目顺利进行,决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费y1与仓库到车站的距离成反比,而每月车载货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
| A.5千米处 | B.4千米处 | C.3千米处 | D.2千米处 |
A
解析试题分析:设仓库到车站的距离是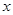 千米,那么有
千米,那么有 ,
,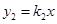 ,将
,将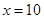 ,
, ,
,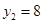 分别代入两个式子,可得
分别代入两个式子,可得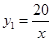 ,
,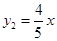 ,所以
,所以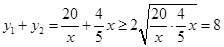 ,当且仅当
,当且仅当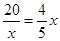 ,即
,即 时,等号成立,所以要使这两项费用之和最小,仓库应建在离车站5千米处.
时,等号成立,所以要使这两项费用之和最小,仓库应建在离车站5千米处.
考点:基本不等式及其应用

练习册系列答案
相关题目
已知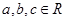 ,给出下列命题:
,给出下列命题:
①若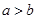 ,则
,则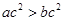 ;②若ab≠0,则
;②若ab≠0,则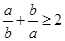 ;③若
;③若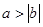 ,则
,则 ;
;
其中真命题的个数为( )
| A.3 | B.2 | C.1 | D.0 |
设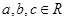 ,且
,且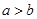 ,则( )
,则( )
A.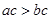 | B.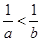 | C.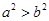 | D.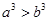 |
若不等式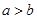 与
与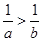 同时成立,则必有( )
同时成立,则必有( )
A.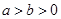 | B.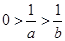 | C.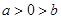 | D.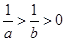 |
对于使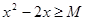 成立的所有常数M中,我们把M的最大值-1,称为函数
成立的所有常数M中,我们把M的最大值-1,称为函数 的“下确界”,若
的“下确界”,若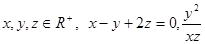 的“下确界”为
的“下确界”为
| A.8 | B.6 | C. 4 | D.1 |
设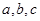 都是正数,
都是正数,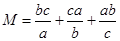 ,
,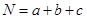 ,则
,则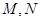 的大小关系是 ( ).
的大小关系是 ( ).
A. | B. | C.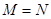 | D.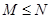 |
若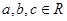 ,且
,且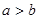 ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )
A.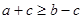 | B.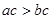 |
C.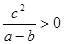 | D.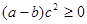 |
设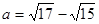 ,
,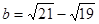 ,
,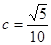 ,则
,则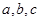 的大小关系为
的大小关系为
A.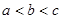 | B. | C.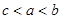 | D.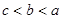 |
要证明a2+b2-1-a2b2≤0,只要证明( )
| A.2ab-1-a2b2≤0 | B.a2+b2-1- ≤0 ≤0 |
C.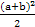 -1-a2b2≤0 -1-a2b2≤0 | D.(a2-1)(b2-1)≥0 |