题目内容
8.设f(x)是定义在[1,+∞)的函数,对任意正实数x,f(3x)=3f(x),且f(x)=1-|x-2|,1≤x≤3,则使得f(x)=f(2015)的最小实数x为( )| A. | 172 | B. | 415 | C. | 557 | D. | 89 |
分析 根据条件先求出f(2015)=172,然后根据条件求出分段函数在每一段上的最大值,然后只需找到相应的那个区间即可求出来.
解答 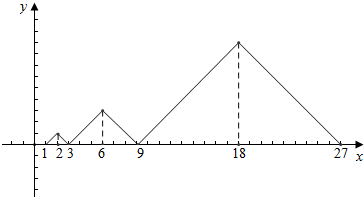 解:因为f(x)对于所有的正实数x均有f(3x)=3f(x),
解:因为f(x)对于所有的正实数x均有f(3x)=3f(x),
所以f(x)=3f($\frac{x}{3}$),
所以f(2015)=3f($\frac{2015}{3}$)=32f($\frac{2015}{{3}^{2}}$)=…=3nf($\frac{2015}{{3}^{n}}$),
当n=6时,$\frac{2015}{{3}^{6}}$∈(1,3),
所以f(2015)=36[1-$\frac{2015}{{3}^{6}}$+2]=37-2015=172,
同理f(x)=3nf($\frac{x}{{3}^{n}}$)=$\left\{\begin{array}{l}{{3}^{n}[1-(\frac{x}{{3}^{n}}-2)],2≤\frac{x}{{3}^{n}}≤3}\\{{3}^{n}[1+(\frac{x}{{3}^{n}}-2)],1≤\frac{x}{{3}^{n}}<2}\end{array}\right.$=$\left\{\begin{array}{l}{{3}^{n+1}-x,2≤\frac{x}{{3}^{n}}≤3}\\{x-{3}^{n},1≤\frac{x}{{3}^{n}}<2}\end{array}\right.$,(n∈N*)
∵f(2)=1,∴f(6)=3f(2)=3,f(18)=3f(6)=32=9,
f(54)=3f(18)=33=27,f(162)=3f(54)=34=81,
f(486)=3f(162)=35=243,
即此时由f(x)=35f($\frac{x}{{3}^{5}}$)=35($\frac{x}{{3}^{5}}$-1)=x-35=172
得x=35+172=243+172=415,
即使得f(x)=f(2015)的最小实数x为415,
故选:B.
点评 本题应属于选择题中的压轴题,对学生的能力要求较高,解决问题的关键在于如何将f(2015)转化到[1,3]上求出它的函数值,二是如何利用方程思想构造方程,按要求求出x的值.

| A. | (-∞,1) | B. | (1,+∞) | C. | $(\frac{2}{3},2)$ | D. | (2,+∞) |