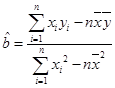题目内容
假设关于某设备的使用年限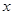 和所支出的维修费用
和所支出的维修费用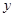 (万元)统计数据如下:
(万元)统计数据如下:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
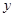 对
对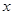 呈线性相关关系.求:
呈线性相关关系.求:(1) 求出线性回归方程
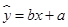 的回归系数;
的回归系数;(2) 估计使用10年时,维修费用是多少。
(1)y=1.23x+0.08;(2)12.38(万元)
解析试题分析:(1)由题意求得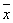 =4,
=4,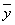 =5,
=5, =1xi2=90,
=1xi2=90,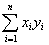 =112.3,于是
=112.3,于是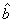 =
=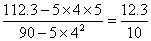 =1.23,
=1.23,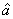 =
=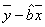 =5-1.23×4=0.08.
=5-1.23×4=0.08.
(2)回归直线方程是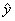 =1.23x+0.08,当x=10(年)时,
=1.23x+0.08,当x=10(年)时,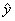 =1.23×10+0.08=12.38(万元),即估计使用10年时维修费用是12.38万元.
=1.23×10+0.08=12.38(万元),即估计使用10年时维修费用是12.38万元.
考点:本题考查了线性回归直线方程的求法及应用
点评:求回归直线方程的步骤是:①作出散点图,判断散点是否在一条直线附近;②如果散点在一条直线附近,由公式求出a、b的值,并写出线性回归方程

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(1)求每个报名者能被聘用的概率;
(2)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(3)公司从聘用的四男
 、
、 、
、 、
、 和二女
和二女 、
、 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
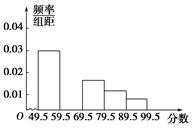
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? 电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图: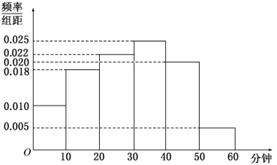
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |
附:K2=
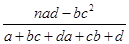 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取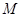 名学生作为样本,得到这
名学生作为样本,得到这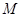 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
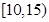 | 10 | 0.25 |
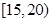 | 24 | 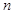 |
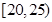 | 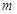 | 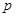 |
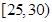 | 2 | 0.05 |
| 合计 | 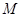 | 1 |
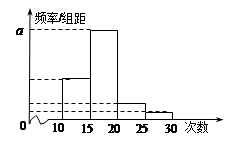
(Ⅰ)求出表中
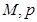 及图中
及图中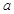 的值;
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
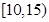 内的人数;
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
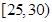 内的概率.
内的概率. (本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 | 403 | 390 | 397 | 404 | 388 | 400 | 412 | 406 |
| 乙队 | 417 | 401 | 410 | 416 | 406 | 421 | 398 | 411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
 ,
, ,…,
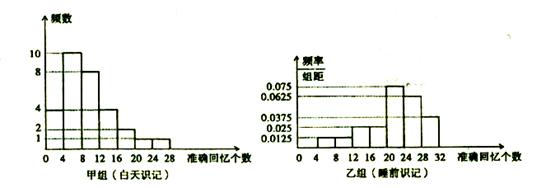
,…, 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: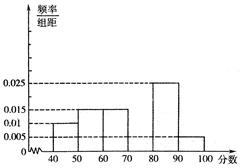
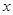 与销售额
与销售额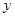 之间有如下的对应数据:
之间有如下的对应数据: