题目内容
（本小题满分10分）
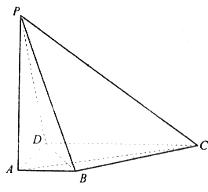
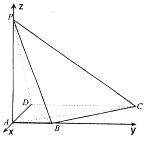
如图，在四棱锥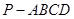
中，底面ABCD为直角梯形，AB∥CD，∠BAD=90°，PA⊥平面ABCD，AB=1，AD=2，PA=CD=4，求二面角
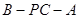的余弦值.
【答案】
二面角B－PC－A的余弦值为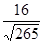
.
【解析】本小题采用向量法求二面角,先求出二面角两个面的法向量,再求法向量的夹角,再根据法向量的夹角与二面角相等或互补来求解.
解：如图建立空间直角坐标系，则A（0，0，0），B（0，1，0），C（－2，4，0），D（－2，0，0），P（0，0，4），易证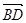
为面PAC的法向量，则
设面PBC的法向量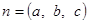
，
，
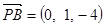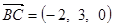
所以
所以面PBC的法向量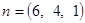
∴
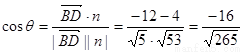
因为面PAC和面PBC所成的角为锐角，所以二面角B－PC－A的余弦值为.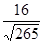
练习册系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，