题目内容
与椭圆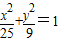 有相同的焦点且离心率为2的双曲线标准方程是 .
有相同的焦点且离心率为2的双曲线标准方程是 .
【答案】分析:求出椭圆 的焦点坐标,设出双曲线的方程,据题意得到参数c的值,根据双曲线的离心率等于2,得到参数a的值,得到双曲线的方程.
的焦点坐标,设出双曲线的方程,据题意得到参数c的值,根据双曲线的离心率等于2,得到参数a的值,得到双曲线的方程.
解答:解:∵椭圆 的焦点坐标为(-4,0)和(4,0),…(1分)
的焦点坐标为(-4,0)和(4,0),…(1分)
设双曲线方程为 (a>0,b>0),
(a>0,b>0),
则c=4,…(2分)
∵双曲线的离心率等于2,即 =2,∴a=2. …(4分)
=2,∴a=2. …(4分)
∴b2=c2-a2=12. …(5分);
故所求双曲线方程为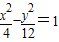 .…(6分).
.…(6分).
故答案为: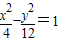 .
.
点评:本题主要考查双曲线的简单性质和标准方程.解答的关键在于考生对圆锥曲线的基础知识的把握.
 的焦点坐标,设出双曲线的方程,据题意得到参数c的值,根据双曲线的离心率等于2,得到参数a的值,得到双曲线的方程.
的焦点坐标,设出双曲线的方程,据题意得到参数c的值,根据双曲线的离心率等于2,得到参数a的值,得到双曲线的方程.解答:解:∵椭圆
 的焦点坐标为(-4,0)和(4,0),…(1分)
的焦点坐标为(-4,0)和(4,0),…(1分)设双曲线方程为
 (a>0,b>0),
(a>0,b>0),则c=4,…(2分)
∵双曲线的离心率等于2,即
 =2,∴a=2. …(4分)
=2,∴a=2. …(4分)∴b2=c2-a2=12. …(5分);
故所求双曲线方程为
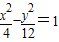 .…(6分).
.…(6分).故答案为:
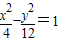 .
.点评:本题主要考查双曲线的简单性质和标准方程.解答的关键在于考生对圆锥曲线的基础知识的把握.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
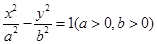 与椭圆
与椭圆 有相同的焦点
有相同的焦点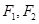 ,且该双曲线
,且该双曲线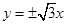 .
. 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点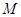 、
、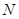 ,
,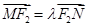 ,当
,当 轴上的点
轴上的点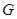 满足
满足 时,求点
时,求点 有相同的焦点且以
有相同的焦点且以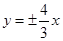 为渐近线的双曲线方程为 .
为渐近线的双曲线方程为 .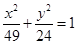 有相同的焦点且以
有相同的焦点且以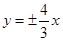 为渐近线的双曲线方程 .
为渐近线的双曲线方程 .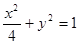 有相同的焦点且过点P
有相同的焦点且过点P 的双曲线方程是
的双曲线方程是  有相同的焦点且离心率为2的双曲线标准方程是 .
有相同的焦点且离心率为2的双曲线标准方程是 .