题目内容
(本题满分12分)设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线交
垂直的直线交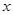 轴负半轴于点
轴负半轴于点 ,且
,且 .
.
(1)求椭圆 的离心率; (2)若过
的离心率; (2)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,
相切,
求椭圆 的方程;
的方程;
【答案】
(1)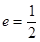 ;(2)
;(2)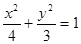 。
。
【解析】
试题分析:(1)设Q(x0,0),由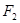 (c,0),A(0,b)
(c,0),A(0,b)
知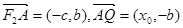
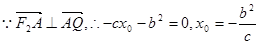 ,
,
由于 即
即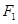 为
为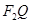 中点.
中点.
故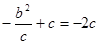
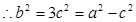 ,
,
故椭圆的离心率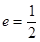 ……6分
……6分
(2)由⑴知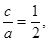 得
得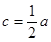 于是
于是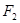 (
(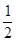
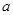 ,0) Q
,0) Q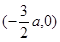 ,
,
△AQF的外接圆圆心为F1(-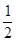
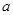 ,0),半径r=
,0),半径r=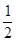 |FQ|=
|FQ|=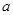
所以 ,解得
,解得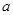 =2,∴c =1,b=
=2,∴c =1,b=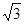 ,
,
所求椭圆方程为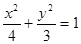 ……12分
……12分
考点:椭圆的简单性质;向量的运算;直线与圆的位置关系。
点评:在求椭圆的离心率时,判断出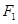 为
为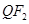 的中点是解题的关键。属于基础题型。在计算时一定要认真、仔细,避免出现计算错误。
的中点是解题的关键。属于基础题型。在计算时一定要认真、仔细,避免出现计算错误。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;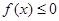 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求