题目内容
设不等式x2-2ax+a+2≤0的解集为M,若M⊆[1,4],求实数a的范围.
分析:M⊆[1,4]有两种情况:其一是M=∅,此时△<0;其二是M≠∅,此时△=0或△>0,分三种情况计算a的取值范围,再取并集,即得所求.
解答:解:M⊆[1,4]有两种情况:其一是M=∅,此时△<0;其二是M≠∅,此时△=0或△>0,
分三种情况计算a的取值范围.
设f (x)=x2-2ax+a+2,有△=(-2a)2-4(a+2)=4(a2-a-2).…(2分)
(1)当△<0时,-1<a<2,M=∅⊆[1,4].…(3分)
(2)当△=0时,a=-1或2.
当a=-1时,M={-1}?[1,4],故舍去.
当a=2时,M={2}⊆[1,4].…(6分)
(3)当△>0时,有a<-1或a>2.
设方程f (x)=0的两根为x1,x2,且x1<x2,
那么M=[x1,x2],由M⊆[1,4]可得 1≤x1<x2≤4,故应有f(1)≥0,f(4)≥0,
且f (x)=0的对称轴x=a∈[1,4],即
,…(8分)
∴
,解得2<a≤
.…(10分)
综上可得,M⊆[1,4]时,a的取值范围是 (-1,
].…(12分)
分三种情况计算a的取值范围.
设f (x)=x2-2ax+a+2,有△=(-2a)2-4(a+2)=4(a2-a-2).…(2分)
(1)当△<0时,-1<a<2,M=∅⊆[1,4].…(3分)
(2)当△=0时,a=-1或2.
当a=-1时,M={-1}?[1,4],故舍去.
当a=2时,M={2}⊆[1,4].…(6分)
(3)当△>0时,有a<-1或a>2.
设方程f (x)=0的两根为x1,x2,且x1<x2,
那么M=[x1,x2],由M⊆[1,4]可得 1≤x1<x2≤4,故应有f(1)≥0,f(4)≥0,
且f (x)=0的对称轴x=a∈[1,4],即
|
∴
|
| 18 |
| 7 |
综上可得,M⊆[1,4]时,a的取值范围是 (-1,
| 18 |
| 7 |
点评:本题主要考查集合关系中参数的取值范围问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
设不等式x2-2ax+a+2≤0的解集为A,若A⊆[1,3],则实数a的取值范围是( )
A、(-1,
| ||
B、(1,
| ||
C、(2,
| ||
| D、(-1,3] |
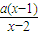 >1(a≠1).
>1(a≠1).