题目内容
设不等式x2-2ax+a+2≤0的解集为M，如果M⊆[1，4]，则实数a的范围是 ．
分析：由已知中关于x的不等式x2-2ax+a+2≤0的解集为M，M⊆[1，4]，根据二次函数的图象和性质，得到满足条件的a的取值范围
解答：解：∵不等式x2-2ax+a+2≤0的解集为M，M⊆[1，4]，
当M=∅时，△=（-2a）2-4（a+2）＜0，
解得，-1＜a＜2；
当M≠∅时，
设f（x）=x2-2ax+a+2，图象是抛物线，开口向上，对称轴是x=a；
∴
，
解得：2≤a≤
，
∴a的取值范围为（-1，2）∪[2，
]=（-1，
]
故答案为：(-1，
]
当M=∅时，△=（-2a）2-4（a+2）＜0，
解得，-1＜a＜2；
当M≠∅时，
设f（x）=x2-2ax+a+2，图象是抛物线，开口向上，对称轴是x=a；
∴
|
解得：2≤a≤
| 18 |
| 7 |
∴a的取值范围为（-1，2）∪[2，
| 18 |
| 7 |
| 18 |
| 7 |
故答案为：(-1，
| 18 |
| 7 |
点评：本题考查了二次函数的图象与性质，解题时根据二次函数的图象分析M⊆[1，4]时满足的条件，将问题转化解不等式组，是解题的关键．
练习册系列答案
相关题目
设不等式x2-2ax+a+2≤0的解集为A，若A⊆[1，3]，则实数a的取值范围是（ ）
A、（-1，
| ||
B、（1，
| ||
C、（2，
| ||
| D、（-1，3] |
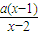＞1（a≠1）．