题目内容
(1)设不等式x2-2ax+a+2≤0的解集为M,如果M⊆[1,4],求实数a的取值范围?(2)解关于x的不等式
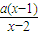 >1(a≠1).
>1(a≠1).
【答案】分析:(1)该题实质上是二次函数的区间根问题,已知M⊆[1,4],首先分类讨论①M=∅,得出△<0,解出a的范围;②M≠∅,此时△=0或△>0,分三种情况计算a的取值范围,然后综合①②的情况求出实数a的取值范围;
(2)先通分为: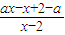 >0,因为方程(x-2)(ax-x+2-a)=0的两根x=2与x=
>0,因为方程(x-2)(ax-x+2-a)=0的两根x=2与x=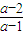 ,大小没法比较,所以要分类讨论,①a>1;②a<1,从而求出不等式的解.
,大小没法比较,所以要分类讨论,①a>1;②a<1,从而求出不等式的解.
解答:解:(1)设f(x)=x2-2ax+a+2,有△=(-2a)2-4(a+2)=4(a2-a-2)
∵M⊆[1,4]有两种情况:
①M=∅,此时△<0;
当△<0时,-1<a<2,M=∅⊆[1,4];
②其二是M≠∅,此时△=0或△>0,分三种情况计算a的取值范围
当△=0时,a=-1或2;
当a=-1时M={-1}?[1,4];
当a=2时,m={2}⊆[1,4].
当△>0时,a<-1或a>2.
设方程f(x)=0的两根x1,x2,且x1<x2,
那么M=[x1,x2],M⊆[1,4]
∴1≤x1<x2≤4,
∴f(1)≥0且f(4)≥0,1≤a≤4,且△>0,
即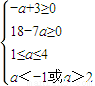 ,解得2<a≤
,解得2<a≤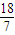 ,
,
综上讨论知,当M⊆[1,4]时,a的取值范围是(-1,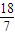 ].
].
(2)原不等式可化为: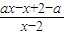 >0,
>0,
①当a>1时,原不等式与(x-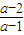 )(x-2)>0同解.
)(x-2)>0同解.
由于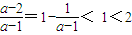 ,
,
∴原不等式的解为(-∞,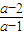 )∪(2,+∞).
)∪(2,+∞).
②当a<1时,原不等式与(x-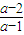 )(x-2)<0同解.
)(x-2)<0同解.
由于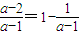 ,
,
若a<0,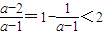 ,解集为(
,解集为( ,2);
,2);
若a=0时,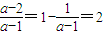 ,解集为∅;
,解集为∅;
若0<a<1,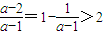 ,解集为(2,
,解集为(2,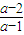 ,).
,).
综上所述:当a>1时解集为(-∞,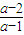 )∪(2,+∞);
)∪(2,+∞);
当0<a<1时,解集为(2,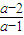 );
);
当a=0时,解集为∅;当a<0时,解集为(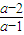 ,2).
,2).
点评:此题主要考查一元二次不等式的解法,运用了分类讨论的思想,分类讨论的问题比较多,从而加大了试题的难度.
(2)先通分为:
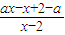 >0,因为方程(x-2)(ax-x+2-a)=0的两根x=2与x=
>0,因为方程(x-2)(ax-x+2-a)=0的两根x=2与x=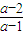 ,大小没法比较,所以要分类讨论,①a>1;②a<1,从而求出不等式的解.
,大小没法比较,所以要分类讨论,①a>1;②a<1,从而求出不等式的解.解答:解:(1)设f(x)=x2-2ax+a+2,有△=(-2a)2-4(a+2)=4(a2-a-2)
∵M⊆[1,4]有两种情况:
①M=∅,此时△<0;
当△<0时,-1<a<2,M=∅⊆[1,4];
②其二是M≠∅,此时△=0或△>0,分三种情况计算a的取值范围
当△=0时,a=-1或2;
当a=-1时M={-1}?[1,4];
当a=2时,m={2}⊆[1,4].
当△>0时,a<-1或a>2.
设方程f(x)=0的两根x1,x2,且x1<x2,
那么M=[x1,x2],M⊆[1,4]
∴1≤x1<x2≤4,
∴f(1)≥0且f(4)≥0,1≤a≤4,且△>0,
即
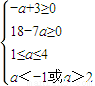 ,解得2<a≤
,解得2<a≤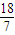 ,
,综上讨论知,当M⊆[1,4]时,a的取值范围是(-1,
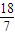 ].
].(2)原不等式可化为:
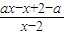 >0,
>0,①当a>1时,原不等式与(x-
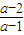 )(x-2)>0同解.
)(x-2)>0同解.由于
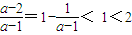 ,
,∴原不等式的解为(-∞,
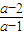 )∪(2,+∞).
)∪(2,+∞).②当a<1时,原不等式与(x-
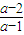 )(x-2)<0同解.
)(x-2)<0同解.由于
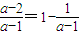 ,
,若a<0,
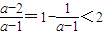 ,解集为(
,解集为( ,2);
,2);若a=0时,
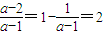 ,解集为∅;
,解集为∅;若0<a<1,
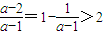 ,解集为(2,
,解集为(2,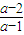 ,).
,).综上所述:当a>1时解集为(-∞,
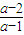 )∪(2,+∞);
)∪(2,+∞);当0<a<1时,解集为(2,
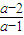 );
);当a=0时,解集为∅;当a<0时,解集为(
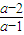 ,2).
,2).点评:此题主要考查一元二次不等式的解法,运用了分类讨论的思想,分类讨论的问题比较多,从而加大了试题的难度.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目