题目内容
【题目】已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足 ![]() =
= ![]() (0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( ) 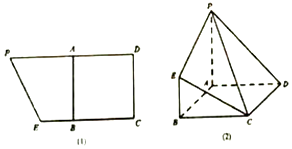
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:由题意,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系, 则D(0,4,0),E(4,0,2),C(4,4,0),P(0,0,4),A(0,0,0),B(4,0,0),
设F(t,0,0),0≤t≤4, ![]() =
= ![]() (0<λ<1),
(0<λ<1),
则(t,0,0)=(4λ,0,0),∴t=4λ,∴F(4λ,0,0),![]() =(4,﹣4,2),
=(4,﹣4,2), ![]() =(4λ,﹣4,0),
=(4λ,﹣4,0), ![]() =(4,4,﹣4),
=(4,4,﹣4), ![]() =(4,0,﹣2),
=(4,0,﹣2),
设平面DEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 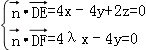 ,取x=1,得
,取x=1,得 ![]() =(1,λ,2λ﹣2),
=(1,λ,2λ﹣2),
设平面PCE的法向量 ![]() =(a,b,c),
=(a,b,c),
则 ![]() ,取a=1,得
,取a=1,得 ![]() =(1,1,2),
=(1,1,2),
∵平面DEF⊥平面PCE,
∴ ![]() =1+λ+2(2λ﹣2)=0,解得
=1+λ+2(2λ﹣2)=0,解得 ![]() .
.
故选:C.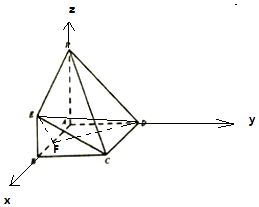
【考点精析】关于本题考查的平面与平面垂直的性质,需要了解两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直才能得出正确答案.

练习册系列答案
相关题目
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程 ![]() =
= ![]() t+
t+ ![]() .
.
(Ⅱ)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() =
= ![]() t+
t+ ![]() 中
中 .
.