题目内容
已知点A(2,0),B(-1,
)是圆x2+y2=4上的定点,经过点B的直线与该圆交于另一点C,当△ABC面积最大时,直线BC的方程为______.
| 3 |
由题意,当△ABC面积最大时,C到AB的距离最大,设C(2cosα,2sinα),则
∵点A(2,0),B(-1,
),
∴直线AB的方程为x-
y-2=0,
∴C到AB的距离为
=|2cos(α+
)-1|,
∴cos(α+
)=-1时,C到AB的距离最大为3,此时α可取
,
∴C(-1,-
),
∵B(-1,
),直线BC的方程为x=-1.
故答案为:x=-1.
∵点A(2,0),B(-1,
| 3 |
∴直线AB的方程为x-
| 3 |
∴C到AB的距离为
|2cosα-2
| ||
|
| π |
| 3 |
∴cos(α+
| π |
| 3 |
| 2π |
| 3 |
∴C(-1,-
| 3 |
∵B(-1,
| 3 |
故答案为:x=-1.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 .
.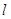 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线 是曲线C上的动点,求
是曲线C上的动点,求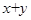 的最大值.
的最大值.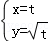 (t为参数)和
(t为参数)和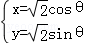 (θ为参数),则曲线C1与C2的交点坐标为 _________ .
(θ为参数),则曲线C1与C2的交点坐标为 _________ .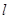 的参数方程是
的参数方程是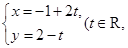
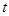 是参数),则直线
是参数),则直线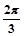 ,1)对应点的直角坐标是__________.
,1)对应点的直角坐标是__________. 和
和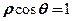 相交于点A、B,则
相交于点A、B,则 =
=