题目内容

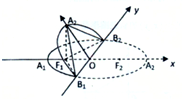如图，椭圆
x2
16
+
y2
12
=1的长轴为A1A2，短轴为B1B2，将坐标平面沿y轴折成一个二面角，使点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点，则此二面角的大小为
π
3
π
3
．
分析：确定椭圆中的几何量，确定二面角的平面角，利用点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点，可求得cos∠A2OF1=
c
a
=
1
2
，即可求得结论．
解答：解：由题意，椭圆
x2
16
+
y2
12
=1中a=4，c=
a2-b2
=2，∠A2OF1为二面角的平面角
∵点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点
∴在直角△A2OF1中，cos∠A2OF1=
c
a
=
1
2

∴∠A2OF1=
π
3

即二面角的大小为
π
3

故答案为：
π
3
点评：本题考查椭圆与立体几何的综合，考查面面角，解题的关键是确定二面角的平面角．
练习册系列答案
相关题目
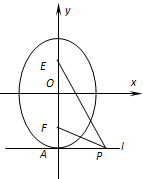精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
精英家教网（1）已知平面上两定点A（-2，0）．B（2，0），且动点M标满足
MA
•
MB
=0，求动点M的轨迹方程；
（2）若把（1）的M的轨迹图象向右平移一个单位，再向下平移一个单位，恰与直线x+ky-3=0 相切，试求实数k的值；
（3）如图，l是经过椭圆
y2
25
+
x2
16
=1长轴顶点A且与长轴垂直的直线，E．F是两个焦点，点P∈l，P不与A重合．若∠EPF=α，求α的取值范围．
并将此题类比到双曲线：
y2
25
-
x2
16
=1，l是经过焦点F且与实轴垂直的直线，A、B是两个顶点，点P∈l，P不与F重合，请作出其图象．若∠APB=α，写出角α的取值范围．（不需要解题过程）
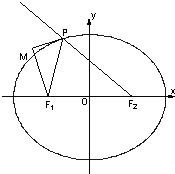精英家教网已知如图，椭圆方程为
x2
16
+
y2
b2
=1（4＞b＞0）．P为椭圆上的动点，
F1、F2为椭圆的两焦点，当点P不在x轴上时，过F1作∠F1PF2的外角
平分线的垂线F1M，垂足为M，当点P在x轴上时，定义M与P重合．
（1）求M点的轨迹T的方程；
（2）已知O（0，0）、E（2，1），试探究是否存在这样的点Q：Q是轨迹T内部的整点（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积S△OEQ=2？若存在，求出点Q的坐标，若不存在，说明理由．
如图，椭圆C：
x2
16
+
y2
4
=1的右顶点是A，上下两个顶点分别为B，D，四边形DAMB是矩形（O为坐标原点），点E，P分别是线段OA，MA的中点．
（1）求证：直线DE与直线BP的交点在椭圆C上．
（2）过点B的直线l1，l2与椭圆C分别交于R，S（不同于B点），且它们的斜率k1，k2满足k1•k2=-
1
4
求证：直线SR过定点，并求出此定点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网