��Ŀ����
��ͼ����֪˫����C1��
-y2=1������C2��|y|=|x|+1��P��ƽ����һ�㣬�����ڹ���P��ֱ����C1��C2���й����㣬���PΪ��C1-C2�͵㡰
��1������ȷ֤��C1�����ǡ�C1-C2�͵㡰ʱ��Ҫʹ��һ�����ý����ֱ�ߣ���д��һ��������ֱ�ߵķ��̣���Ҫ����֤����
��2����ֱ��y=kx��C2�й����㣬��֤|k|��1������֤��ԭ�㲻�ǡ�C1-C2�͵㡱��
��3����֤��Բx2+y2=
�ڵĵ㶼���ǡ�C1-C2�͵㡱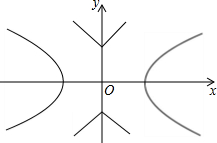
| x2 |
| 2 |
��1������ȷ֤��C1�����ǡ�C1-C2�͵㡰ʱ��Ҫʹ��һ�����ý����ֱ�ߣ���д��һ��������ֱ�ߵķ��̣���Ҫ����֤����
��2����ֱ��y=kx��C2�й����㣬��֤|k|��1������֤��ԭ�㲻�ǡ�C1-C2�͵㡱��
��3����֤��Բx2+y2=
| 1 |
| 2 |

��1��C1������-
��0����д����ֱ�߷��̿�����������ʽ��
x=-
��y=k(x+
)������|k|��
��
��2��֤������Ϊֱ��y=kx��C2�й����㣬
���Է�����
��ʵ���⣬���|kx|=|x|+1����|k|=
��1��
��ԭ���ǡ�C1-C2�͵㡱������ڹ�ԭ���ֱ����C1��C2���й����㣮
���ǹ�ԭ����C2�й������ֱ��x=0��y=kx��|k|��1����
��Ȼֱ��x=0��C1�����㣮
���ֱ��Ϊy=kx��|k|��1�������ɷ�����
����x2=
��0��ì�ܣ�
����ֱ��y=kx��|k|��1����C1Ҳ�����㣮
���ԭ�㲻�ǡ�C1-C2�͵㡱��
��3��֤������ԲO��x2+y2=
��ȡԲO�ڵ�һ��Q�����о���Q��ֱ��l��C1��C2���й����㣬��Ȼl����x�ᴹֱ��
�ʿ���l��y=kx+b��
��|k|��1������ԲO��������ƽ����y=x��1��y=-x��1֮�䣬���ԲOҲ����ֱ��y=kx��1��y=-kx��1֮�䣬
�Ӷ���Q����kΪб�ʵ�ֱ��l��C2�����㣬ì�ܣ�����|k|��1��
��Ϊl��C1�ɹ����㣬���Է�����
��ʵ���⣬
�ã�1-2k2��x2-4kbx-2b2-2=0��
��Ϊ|k|��1������1-2k2��0��
��ˡ�=��4kb��2-4��1-2k2����-2b2-2��=8��b2+1-2k2����0��
��b2��2k2-1��
��ΪԲO��Բ�ģ�0��0����ֱ��l�ľ���d=
��
����
=d2��
���Ӷ�
��b2��2k2-1����k2��1����|k|��1ì�ܣ�
��ˣ�Բx2+y2=
�ڵĵ㲻�ǡ�C1-C2�͵㡱��
| 3 |
x=-
| 3 |
| 3 |
| ||
| 3 |
��2��֤������Ϊֱ��y=kx��C2�й����㣬
���Է�����
|
| |x|+1 |
| |x| |
��ԭ���ǡ�C1-C2�͵㡱������ڹ�ԭ���ֱ����C1��C2���й����㣮
���ǹ�ԭ����C2�й������ֱ��x=0��y=kx��|k|��1����
��Ȼֱ��x=0��C1�����㣮
���ֱ��Ϊy=kx��|k|��1�������ɷ�����
|
| 2 |
| 1-2k2 |
����ֱ��y=kx��|k|��1����C1Ҳ�����㣮
���ԭ�㲻�ǡ�C1-C2�͵㡱��
��3��֤������ԲO��x2+y2=
| 1 |
| 2 |
�ʿ���l��y=kx+b��
��|k|��1������ԲO��������ƽ����y=x��1��y=-x��1֮�䣬���ԲOҲ����ֱ��y=kx��1��y=-kx��1֮�䣬
�Ӷ���Q����kΪб�ʵ�ֱ��l��C2�����㣬ì�ܣ�����|k|��1��
��Ϊl��C1�ɹ����㣬���Է�����
|
�ã�1-2k2��x2-4kbx-2b2-2=0��
��Ϊ|k|��1������1-2k2��0��
��ˡ�=��4kb��2-4��1-2k2����-2b2-2��=8��b2+1-2k2����0��
��b2��2k2-1��
��ΪԲO��Բ�ģ�0��0����ֱ��l�ľ���d=
| |b| | ||
|
����
| b2 |
| 1+k2 |
| 1 |
| 2 |
| 1+k2 |
| 2 |
��ˣ�Բx2+y2=
| 1 |
| 2 |

��ϰ��ϵ�д�
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
�����Ŀ
 ��ͼ����֪˫����C1��
��ͼ����֪˫����C1�� ��2013•�Ϻ�����ͼ����֪˫����C1��
��2013•�Ϻ�����ͼ����֪˫����C1��
 ������C2��|y|=|x|+1��P��ƽ����һ�㣬�����ڹ���P��ֱ����C1��C2���й����㣬���PΪ��C1��C2�͵㡰
������C2��|y|=|x|+1��P��ƽ����һ�㣬�����ڹ���P��ֱ����C1��C2���й����㣬���PΪ��C1��C2�͵㡰
 �ڵĵ㶼���ǡ�C1��C2�͵㡱
�ڵĵ㶼���ǡ�C1��C2�͵㡱