题目内容
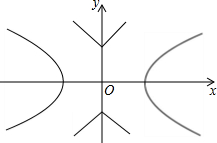
如图，已知双曲线C1:
，曲线C2:
.P是平面内一点.若存在过点P的直线与C1、C2都有共同点，则称P为“C1-C2型点”.
（1）在正确证明C1的左焦点是“C1-C2型点”时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；
（2）设直线y=kx与C2有公共点，求证
＞1，进而证明圆点不是“C1-C2型点”；
（3）求证：圆
内的点都不是“C1-C2型点”.
【答案】 （1） 
【解析】 （1） 
显然，由双曲线
的几何图像性质可知，过
.从曲线
图像上取点P(0,1),则直线
。这时直线方程为
（2） 先证明“若直线y=kx与
有公共点，则＞1”.
双曲线
.
.
所以直线y=kx与有公共点，则＞1 . （证毕）
。
所以原点不是“C1-C2型点”；（完）
（3）设直线
过圆
内一点，则直线斜率不存在时与曲线
无交点。
设直线方程为：y = kx + m，则：
假设直线与曲线相交上方，则
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
如图，已知双曲线C1：
（2013•上海）如图，已知双曲线C1：
，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1﹣C2型点“
内的点都不是“C1﹣C2型点”