题目内容
如图,已知△OFQ的面积为S,且 ·
· =1.设|
=1.设| |=c(c≥2),S=
|=c(c≥2),S= c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当|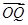 |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
 =1
=1
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
题目内容
如图,已知△OFQ的面积为S,且 ·
· =1.设|
=1.设| |=c(c≥2),S=
|=c(c≥2),S= c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当|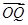 |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
 =1
=1
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案