题目内容
若直线a与b是异面直线,直线b与c是异面直线,则直线a与c( )
分析:在正方体ABCD-A′B′C′D′中,分别找出满足条件直线a与b是异面直线,直线b与c是异面直线的直线,借助正方体的几何特征易分析出答案.
解答:解:在正方体ABCD-A′B′C′D′中,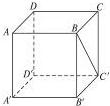
令直线a为AA′,直线b为CD,直线c为BB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c平行;
令直线a为AA′,直线b为CD,直线c为AB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c相交;
令直线a为AA′,直线b为CD,直线c为DB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c异面;
故直线a与c可能平行,可能相交,也可能异面,
故选D

令直线a为AA′,直线b为CD,直线c为BB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c平行;
令直线a为AA′,直线b为CD,直线c为AB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c相交;
令直线a为AA′,直线b为CD,直线c为DB′,满足直线a与b是异面直线,直线b与c是异面直线,此时直线a与c异面;
故直线a与c可能平行,可能相交,也可能异面,
故选D
点评:本题考查的知识点是异面直线的判定,空间直线与直线的位置关系,其中以正方体的研究对象将抽象问题具体化是解答的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

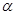 ,则
,则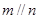
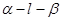 是直二面角,若直线
是直二面角,若直线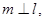 则
则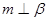
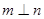 ,则
,则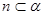 或
或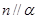
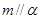 ,则n与
,则n与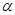 ,则
,则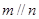
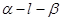 是直二面角,若直线
是直二面角,若直线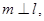 则
则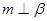
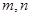 在平面
在平面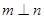 ,则
,则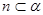 或
或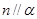
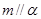 ,则n与
,则n与